avec n =
Retour au plan du
cours de Chimie.
Ces manipulations, du moins les 12 premières, ont
été mises au point (recherche bibliographique, ajustement
des mesures, etc...) par Jean MUSSO et Edmond LANZA dans les années
70. Qu' ils en soient ici remerciés.
Les autres manipulations sont le fruit de recherches
personnelles et d' échanges de manipulations entre divers
collègues d' universités françaises ou étrangères.
Le but de ce site étant de pouvoir alimenter un fonds commun servant
à toutes et à tous, et non pas de dire : "C' est moi
qui ai tout inventé."
Le niveau des manips dépasse parfois le niveau
DEUG. Cela sera bien entendu indiqué à l' étudiant.
Ce sont des TP "must" qu' il faut avoir fait au moins
une fois dans sa vie et qui sont, par conséquent, incontournables:
même un Prix NOBEL de chimie ne peut pas faire l' impasse sur la
détermination rigoureuse d' une concentration de solution
aqueuse d' hydroxyde de sodium!
Je me suis contenté de réactualiser certains commentaires (la notion de "normalité" est tout à fait inutile par exemple, car c' est un sac de noeuds invraisemblable; d' autant plus que la notion de concentration est universelle et "puissante") et j' ai insisté sur des points d' achoppement permanents, récurrents, de la part des étudiants de DEUG, et ce, quels que soient leur niveau et/ou leur baccalauréat.
Que ceux qui ont tout compris tout de suite me pardonnent mes redondances!! F.M.
Notions sur les calculs d' incertitude appliqués à la chimie.
Notions sur les équations aux dimensions.
Manipulation 1: acidimétrie. Mesures volumétriques.
Manipulation 2: alcalimétrie. Mesures volumétriques.
Manipulation 3: manganimétrie. Mesures volumétriques.
Manipulation 4: iodométrie. Mesures volumétriques.
Manipulation 5: les pH des solutions aqueuses. Mesures potentiométriques.
Manipulation 6: potentiel d' oxydoréduction. Mesures potentiométriques.
Manipulation 7: cinétique chimique du premier ordre.
Manipulation 8: cinétique chimique du deuxième ordre.
Manipulation 10: recherche des anions d' une solution aqueuse.
Manipulation 11: recherche des cations d' une solution aqueuse.
Manipulation 13: complexométrie.
Manipulation 14: diagramme potentiel-pH du système fer-eau.
Manipulation 18: chromatographies.
Manipulation 19: détermination par spectrophotométrie visible du pKa d' un indicateur coloré.
Manipulation 20: dosage des constituants d' un ciment.
Retour au sommaire des TP de Chimie.
Retour au sommaire de la méthodologie chimie.
Soit à calculer l' incertitude sur la concentration
C d' une substance X, déterminée à partir d' une pesée
d' une masse m de X, dissoute dans un volume V.
Par définition, la concentration C de la substance
X est égale à:
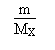
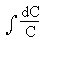 est
égal à Ln
est
égal à LnOn passera ensuite aux quantités finies: les erreurs
s' ajoutant, on remplace les signes "moins" par des signes "plus".
On obtient alors:
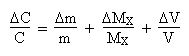
Application numérique:
Soit une masse pesée de chlorure de sodium, NaCl,
de masse molaire égale à 58.5 g.mol-1, égale
à 2.0045 g, dissoute dans une fiole jaugée de volume
V égal à 100 mL.
Quelle est la concentration, exprimée en mol.L-1,
de la solution de chlorure de sodium, et quelle est l' incertitude sur
la mesure de la concentration?
On donne, pour répondre à la question posée,
comme incertitude sur le volume de la fiole jaugée, la valeur DV
égale à 0.1 mL.
L' incertitude absolue Dm
sur la masse pesée est égale à 0.0001 g.
L' incertitude relative![]() sur la masse molaire du chlorure de sodium est égale à 0.2
%, comme d' habitude avec les produits de l' UTV.
sur la masse molaire du chlorure de sodium est égale à 0.2
%, comme d' habitude avec les produits de l' UTV.
En théorie c' est la valeur la MOINS PRECISE dans toute une série de valeurs qui IMPOSE sa précision à l' ensemble du calcul.
Le calcul de la concentration en chlorure de sodium conduit à une valeur de: 0.343 mol.L-1. Cette valeur est choisie car elle comporte trois chiffres significatifs, ce nombre étant celui donné par la masse molaire de NaCl, 58.5 g.mol-1, valeur la "moins" précise parmi toutes celles fournies.
Le calcul sur la valeur de l' incertitude absolue DC sur cette même concentration est égal à: 0.001 mol.L-1. On ne retient ici que trois chiffres significatifs étant donné que le calcul de C ne donne que trois chiffres significatifs.
Si l' on donne un résultat avec trois chiffres après la virgule pour la valeur de C il ne faut pas avoir seulement 1 chiffre après la virgule pour DC, ou, tout aussi pire, DIX chiffres après la virgule pour DC. Il s' agit d' une question d' HOMOGENEITE des résultats.
A partir de là on fournit un résultat concernant la mesure sous la forme:
Une fois qu' on a calculé l' incertitude absolue
DCa,
sur la concentration Ca d' une substance, ce calcul va désormais
servir, en cascade, à déterminer d' autres incertitudes sur
d' autres résultats.
La plupart des calculs de concentration se ramènent
à des formules simples du type:
a.Ca.Va = b.Cb.Vb
Les coefficients a et b, désignent les coefficients stoechiométriques dans l' équation globale de dosage faisant intervenir l' espèce a avec l' espèce b. Ils peuvent être, dans les cas les plus triviaux , égaux à 1 tous les deux (par exemple le fameux dosage de l' acide chlorhydrique par la soude), ou non tous égaux à 1: cas le plus fréquent, notamment en oxydoréduction, ou lors du dosage d' un polyacide par une monobase....
Imaginons que nous cherchions à calculer la valeur
de Cb, et celle de DCb, connaissant Ca et DCa,
déterminées précédemment.
La valeur de Cb se calcule aisément par la formule
précédente a.Ca.Va = b.Cb.Vb
Il suffit d' extraire Cb.
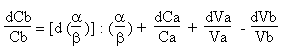
Comme la différentielle d' une constante (à savoir le rapport a/b) est égale à 0, au niveau du calcul d' incertitude sur DCb tout se passe comme si l' on n' avait pas eu de coefficients stoechiométriques différents de l' unité dans la formule de calcul a.Ca.Va = b.Cb.Vb
![]()
Bien entendu, pour calculer Cb les coefficients stoechiométriques s' avèrent nécessaires!!!
Incertitudes absolues sur les différents
éléments de verrerie:
| Matériel de verrerie | Incertitude absolue |
| Burette de 25 mL | DV = 0.05 mL |
| Fiole jaugée de 250 mL | DV = 0.15 mL |
| Fiole jaugée de 200 mL | DV = 0.15 mL |
| Fiole jaugée de 100 mL | DV = 0.10 mL |
| Pipette jaugée de 5 mL | DV = 0.02 mL |
| Pipette jaugée de 10 mL | DV = 0.05 mL |
| Pipette jaugée de 20 mL | DV = 0.10 mL |
| Erlenmeyer | Ne constitue pas un élément de précision au cours du dosage |
| Becher | Ne constitue pas un élément de précision au cours du dosage |
| Verre à pied | Ne constitue pas un élément de précision au cours du dosage |
| Eprouvette | Ne constitue pas un élément de précision au cours du dosage |
| Tube à essais | Ne constitue pas un élément de précision au cours du dosage |
| Ampoule à décanter | Ne constitue pas un élément de précision au cours du dosage |
| Ampoule à brome | Ne constitue pas un élément de précision au cours du dosage |
Retour au sommaire des TP de Chimie.
Retour au sommaire de la méthodologie chimie.
Retour au sommaire des TP de Chimie.
Retour au sommaire de la méthodologie chimie.
Les grandeurs physiques sont exprimées, sans exception, à partir des cinq grandeurs fondamentales: la longueur, notée L, la masse, notée M, le temps, noté T, l' intensité du courant électrique, notée I, et la mole, notée mol.
Ainsi, un volume V est homogène à une longueur L à la puissance 3:
Le recours à ce décorticage des grandeurs physiques permet de vérifier la notion très importante de l' homogénéité des formules: est ce que, par exemple, des joules sont homogènes à des kg.m2.s-1 ou pas?
Il faut répondre en disant qu' une énergie, par exemple mesurée en joules, est homogène à une force multipliée par un déplacement.
Le déplacement est homogène à une longueur L donc on arrête là pour lui.
La force, elle, n' est pas une grandeur fondamentale mais une grandeur composée.
Une force est homogène à une masse que multiplie une accélération.
Une masse est une grandeur fondamentale, on la note M. On arrête là pour la masse.
Une accélération est une grandeur composée. C' est une vitesse divisée par un temps T.
Comme la vitesse est également une grandeur composée on la décompose en distance L divisée par un temps T, soit L1.T-1.
On ne peut pas aller plus loin dans la décomposition.
D' où l' accélération est homogène
à L1.T-2.
D' où la force est homogène à M1.L1.T-2.
D' où l' énergie est homogène à
M1.L2.T-2 soit, plus simplement écrit:
M.L2.T-2.
Donc, en accord avec l' équation aux dimensions pour l' énergie, l' énergie est homogène à des kilogrammes.mètres carrés.secondes puissance moins deux, soit à des kg1.m2.s-2 c' est à dire, bien plus simplement , à des kg.m2.s-2.
On constate alors que les joules ne peuvent EN AUCUN CAS être homogènes à des kg.m2.s-1 comme il était demandé dans la question.
Une autre question pratique qui se pose souvent, notamment en TP, est la suivante: comment transformer une sous-unité en une autre, sans que pour autant on ait à recourir à la décomposition de chaque unité dans les composantes fondamentales?
Par exemple comment transformer, en conductimétrie, des microsiemens par centimètre en siemens par mètre, c' est à dire passer des mS.cm-1 en S.m-1 ?
Sans pour autant aller exprimer les siemens dans les cinq unités fondamentales, on se contente ici juste de comparaisons relatives, on remarque que l' unité de mesure étudiée est du type:
[ conductance]1 . [ longueur ]-1 (1)
L' unité de conductance dans le système
international d' unités SI est le siemens, noté S.
L' unité de conductivité dans le
système international SI est le siemens par mètre,
noté S.m-1.
Ici il faut exprimer, en deux temps:
1. Les microsiemens, mS,
en siemens, S.
On a 1 mS
= 10-6 S.
2. Les centimètres, cm, en mètres,
m.
On a 1 cm = 10-2 m.
On reporte ces deux résultats dans la formule (1).
On écrit:
1 mS.cm-1= [10-6 S ]1 . [ 10-2 m ]-1
On développe les puissances à l' intérieur des crochets et on réarrange le résultat. On trouve que:
1 mS.cm-1= 10-4 S.m-1
Après l' effort, le réconfort:
Comment transformer, avec seulement les équations aux dimensions, sinon c' est pas du jeu, des cm3 en m3 ?
Par exemple, combien vaut, en m3, 1 cm3 ?
On reconnaît tout d' abord, un volume, à savoir une grandeur homogène à L3.
On exprime donc une longueur, qui est le centimètre, en mètre, et on porte le résultat au cube:
1 cm3 = [ 10-2 m ]3
On trouve bien évidemment qu' un cm3
vaut 10-6 m3....
Retour au sommaire des TP de Chimie générale.
Retour au sommaire de la méthodologie chimie.
Retour sommaire des TP de
Chimie.
Cette manipulation comporte deux étapes:
1. Etalonnage de la solution titrante de soude à une concentration voisine de 0.1 mol.L-1.
2. Applications:
2.a. Dosage d' une solution aqueuse d' un polyacide,
l' acide phosphorique H3PO4.
2.b. Dosage d' un mélange de deux acides: un monoacide
fort, l' acide chlorhydrique H3O+ + Cl-,
et un polyacide faible, l' acide phosphorique, H3PO4.
Partie 1: étalonnage de la solution de soude.
La solution d' hydroxyde de sodium de titre voisin de 0.1 mol.L-1 est prête. Sa concentration n' est pas rigoureusement connue car la soude est un produit qui se carbonate très facilement à la longue. Elle capte le dioxyde de carbone de l' air et sa concentration en ions hydroxyde s' en trouve modifiée. Il est donc important dans un laboratoire de procéder toujours avant utilisation d' une quelconque solution de soude à son étalonnage préalable.
On remplit dès lors la burette de la solution de
soude fraîchement préparée.
On veillera, et c' est TRES IMPORTANT, à ce qu'
il n' y ait pas de bulles d' air dans le bas de la burette. Une burette
opérationnelle se doit d' être remplie complètement
de liquide depuis le bas du robinet jusqu' à l' orifice de sortie.
Cela n' est point une manie de vieux prof mais simplement le critère
pour que le volume de descente de burette soit rigoureusement celui indiqué
par... la burette.
L' étalonnage sera réalisé ici avec une solution aqueuse d' hydrogénophtalate de potassium (anciennement appelé "phtalate acide de potassium"), de formule semi-développée HO2C-C6H4-CO2K, de formule brute C8H5O4K, cristallisant sans aucune molécule d' eau, de masse molaire M égale à 204.18 g.mol-1. L' hydrogénophtalate de potassium se comportera ici comme un monoacide faible (du fait de la présence de la fonction acide carboxylique) de pKa égal à 5.1 à 25°C.
On préparera 100 mL de solution aqueuse d' hydrogénophtalate de potassium.
La masse m d' hydrogénophtalate de potassium à peser sera calculée de telle façon que 10 mL de solution d' hydrogénophtalate de potassium neutralisent environ 10 mL de solution aqueuse de soude de concentration voisine de 0.1 mol.L-1.
Calculer cette masse m et la peser à la balance de précision.
Remarque: il sera sans doute impossible de peser exactement
la valeur théorique demandée.Ce n' est d' ailleurs pas ce
qui est "demandé", si j' ose dire, en TP.
Si cette valeur théorique fait, admettons, 1.5487
g, il faudra se contenter de peser une masse m voisine de cette masse.
Il faudra peser une masse m comprise, disons, entre 1.5400 g et 1.5500
g.
On notera la valeur réellement pesée pour m.
On calculera la concentration Ca de la solution préparée,
qu' on exprimera en mol.L-1.
On connaît m, on connaît M, et on connaît
V. Jeu d' enfant....
On calculera l' incertitude absolue DCa
sur la concentration calculée Ca et on calculera l' incertitude
relative ![]() sur la mesure. On vérifiera que l' incertitude relative est bien
inférieure à la valeur limite acceptable de 10%.
sur la mesure. On vérifiera que l' incertitude relative est bien
inférieure à la valeur limite acceptable de 10%.
On présentera le résultat sous la formesuivante, en précisant bien l'unité de la concentration:
Une fois la masse m pesée (à l' aide d'
un "sabot" de pesée), verser, à l' aide d' un entonnoir parfaitement
sec, la poudre dans la fiole de 100 mL, elle aussi parfaitement sèche.
Reprendre les grains de poudre restés sur l' entonnoir
par un jet de pissette d' eau distillée, et verser précautionneusement
toutes les gouttes de liquide dans la fiole.
Verser encore une bonne dizaine de mL d' eau sur la poudre,
voire 20 mL, de façon à la dissoudre complètement.
Lorsque la poudre est complètement dissoute dans
l' eau, alors on peut compléter la fiole jusqu' au trait de jauge,
le ménisque du liquide affleurant, par le bas, le trait de jauge.
On agite la fiole, de façon à bien homogénéiser
la solution. La solution étalon, de concentration en hydrogénophtalate
de potassium rigoureusement connue, est désormais prête.
On remplit ensuite un erlenmeyer, qui servira au dosage, de 10 mL (prélevés à la pipette de précision) de solution étalon d' hydrogénophtalate de potassium, de 20 mL d' eau (prélevés à l' éprouvette), et de trois gouttes de phénolphtaléine.
Attention! On ne pipette jamais dans un flacon contenant
un produit.
On verse une partie de la solution à pipeter dans
un bécher et on pipette le volume souhaité à partir
de ce bécher.
On ne remet jamais un liquide versé dans un bécher dans la bouteille d' origine, de façon à éviter les couacs dus à des pollutions malencontreuses. S' il reste du liquide dans le bécher après pipetage il faut le verser dans le jerrican prévu en salle de TP pour les résidus de produits chimiques.
On ne jette rien à l' évier.
On verse goutte à goutte la soude dans l' erlenmeyer jusqu' au virage de la phénolphtaléine de l' incolore au fuchsia.
On note la valeur V du volume équivalent.
On écrit l' équation du dosage qui a eu lieu. On nomme les produits formés.
On calcule la concentration Cb de la soude à partir des valeurs de la concentration Ca de la solution d' hydrogénophtalate de potassium, du volume Va de cette même solution, et du volume V de soude versée à l' équivalence.
On calcule ensuite l' incertitude absolue DCb,
ainsi que l' incertitude relative![]() sur la valeur de la concentration de soude. On utilise les valeurs des
incertitudes sur les différents matériels utilisés
(pipettes, burettes) qui sont donnés en fin de fascicule de TP ou
qui sont donnés en fin de document on line. On vérifie que
l' incertitude relative est bien inférieure à 10%.
sur la valeur de la concentration de soude. On utilise les valeurs des
incertitudes sur les différents matériels utilisés
(pipettes, burettes) qui sont donnés en fin de fascicule de TP ou
qui sont donnés en fin de document on line. On vérifie que
l' incertitude relative est bien inférieure à 10%.
On présentera le résultat sous la forme suivante, en précisant bien l' unité du résultat:
Partie 2: Applications.
2.a. Dosage d' un polyacide faible, l' acide phosphorique, H3PO4.
On dosera l' acide phosphorique en procédant de façon analogue à celle utilisée précédemment.
Prélever 10 mL de solution aqueuse d' acide phosphorique
à l' aide d' une pipette.
Rajouter 20 mL d' eau distillée avec une éprouvette.
Rajouter trois gouttes d' hélianthine.
Effectuer le dosage jusqu' au passage du rouge orangé au jaune de l' indicateur coloré.
Noter le volume V1 de soude versée. Ne pas remettre la burette à zéro, à cause de la suite du dosage.
Ecrire l' équation chimique de salification de
l' acide phosphorique, sachant qu' on s' arrête ici au stade de la
neutralisation de la première fonction acide de l' acide phosphorique.
Nommer les réactifs et les produits formés.
Verser ensuite dans l' erlenmeyer trois gouttes de phénolphtaléine.
Poursuivre le dosage, jusqu' à ce que la solution
passe du jaune au rose.
Noter le volume V2 de soude versée
(en plus du volume V1 initial qui a servi lors de la première
partie du dosage).
Ecrire l' équation chimique qui a eu lieu.
On passe alors à la neutralisation de la seconde
fonction acide de l' acide phosphorique. Bref, et pour ne pas le dire,
on passe de l' anion dihydrogénophosphate à l' anion (mono)hydrogénophosphate.
Déduire, à partir de ces résultats une relation très très simple entre les valeurs de V1 et de V2.
Calculer la concentration Ca de l' acide phosphorique
contenu dans la solution.
Ce n' est pas la peine de tenir compte des 20 mL d' eau
rajoutés à l' aide de l' éprouvette car le résultat
serait faux. Devinez-vous pourquoi?
Calculer l' incertitude absolue DCa
et l' incertitude relative ![]() sur la valeur de la concentration Ca.On utilisera les valeurs des incertitudes
fournies sur les différents matériels de verrerie en fin
de fascicule ou la fin du chapitre on line.
sur la valeur de la concentration Ca.On utilisera les valeurs des incertitudes
fournies sur les différents matériels de verrerie en fin
de fascicule ou la fin du chapitre on line.
Présenter le résultat final sous la forme,
en précisant l' unité du résultat:
2.b. Dosage d' un mélange de deux acides: l' acide chlorhydrique, monoacide fort, et l' acide phosphorique, polyacide faible.
On procédera comme précédemment.
On prendra 10 mL de la solution contenant en mélange
les acides chlorhydrique et phosphorique.Prélèvement à
la pipette. Versement dans un erlenmeyer.
Rajout de 20 mL d' eau distillée. Prélèvement
à l' éprouvette.
Rajout de trois gouttes d' indicateur coloré,
l' hélianthine.
Dosage par la soude.
Premier virage: verser la soude, goutte à goutte, dans l' erlenmeyer, jusqu' au virage de l' indicateur, à savoir passage du rouge orangé au jaune.
Noter le volume V3 de soude qui a été nécessaire.Ne pas remettre la burette à zéro.
Ecrire les deux équations chimiques qui sont
intervenues, sachant que la soude a effectué deux choses distinctes:
1. Neutralisation de tout l' acide chlorhydrique.
2. Neutralisation de la première fonction acide
de l' acide phosphorique.
Nommer dans chaque cas les espèces réagissantes et les espèces formées.
Comme il n' est pas possible de savoir exactement avec ce premier virage combien de soude a réagi avec l' acide chlorhydrique et combien de soude a réagi avec la première acidité de l' acide phosphorique, on fait un deuxième virage, à l' aide d' un second indicateur coloré, la phénolphtaléine.
Verser la soude goutte à goutte, et noter le volume V4, rajouté en supplément du volume V3 du premier dosage, afin d' obtenir la coloration fuchsia.
Ecrire l' équation du dosage qui a lieu, sachant que ce dosage ne concerne que la neutralisation de la seconde fonction acide de l' acide phosphorique. Bref, pour ne pas le dire, on passera de l' anion dihydrogénophosphate à l' anion (mono)hydrogénophosphate.
Nommer les espèces chimiques réagissant et celles qui sont formées.
Calculer, à partir des données, en s' aidant aussi des résultats obtenus lors du dosage de l' acide phosphorique seul, les concentrations des acides chlorhydrique et phosphorique, contenus dans la bouteille sous forme d'un mélange.
Petite mise sur la voie: pour l' une des concentrations
il faudra se servir du volume V4 seulement (en ce qui concerne
la soude versée), alors que pour l' autre concentration il
faudra se servir de la différence
(V3 - V4). Voyez vous pourquoi?
Calculer dès lors l' incertitude absolue DCa
sur la concentration de l' acide phosphorique, ainsi que l' incertitude
relative ![]() .
.
Présenter le résultat sous la forme suivante,
en précisant l' unité du résultat:
Calculer ensuite, de la même façon, l' incertitude absolue DCa', ainsi que l' incertitude relative, sur la concentration de l' acide chlorhydrique.
Présenter le résultat sous la forme suivante, en précisant son unité:
Remarque: durant le TP l' enseignant fera attention à
deux choses importantes avec vous lors du calcul d' incertitude sur les
concentrations de ces deux acides en mélange.
D' une part l' incertitude sur la lecture du volume V4
devra faire apparaître deux fois l' incertitude sur la lecture de
la burette, étant donné que pour lire V4 on fait
une différence de deux lectures, donc deux fois l' erreur de lecture.
D' autre part, le calcul d' incertitude où interviendra la différence de volume (V3-V4) sera fait, au niveau analytique, par l' enseignant. Il s' agit de dériver un produit dans lequel entre en jeu une différence de termes et qui présente une légère difficulté de prime abord. A vous de passer ensuite à l' application numérique.
Retour au sommaire des TP
de Chimie.
Retour sommaire des TP de Chimie
Il s' agit de déterminer la concentration de diverses solutions aqueuses basiques grâce à une solution étalon d' acide chlorhydrique. C' est le "même " TP que le précédent, sauf qu' on remplace les acidespar les bases et vice versa.
Cette manipulation comporte deux étapes fondamentales:
1. Fabrication et étalonnage de la solution aqueuse
d' acide chlorhydrique qui servira pour tous les dosages.
2. Applications.
2.a. Dosage d' une solution aqueuse de carbonate de (di)sodium,
Na2CO3.
2.b. Dosage d' une solution aqueuse appelée communément
"soude carbonatée", à savoir un mélange d' hydroxyde
de sodium NaOH et de carbonate de (di)sodium Na2CO3.
Partie 1: Fabrication de la solution aqueuse d' acide chlorhydrique à étalonner.
On dispose d' une solution aqueuse d' acide chlorhydrique de concentration voisine de 1 mol.L-1.
Préparer, en fonction de la verrerie dont vous disposez, 200 ou 250 mL d' une solution aqueuse d' acide chlorhydrique de concentration égale à 0.2 mol.L-1, environ.
Partie 2: Préparation de la solution aqueuse étalon de carbonate de disodium.
Etant donné que la préparation précédente
ne permet pas de connaître la concentration exacte de l' acide chlorhydrique
préparé, il faut recourir à un étalonnage.
On utilisera pour ce faire du carbonate de (di)sodium
en poudre, dont on préparera une solution de concentration rigoureusement
connue.
Sachant que la masse molaire du carbonate de (di)sodium est égale à 106 g.mol-1, quelle masse m de carbonate de (di)sodium faut-il peser afin de préparer 100 mL d' une solution aqueuse de carbonate de (di)sodium de concentration Cb, concentration Cb telle que 10 mL de cette solution neutraliseront sensiblement le même volume de la solution aqueuse d' acide chlorhydrique de concentration voisine de 0.2 mol.L-1, préparée précédemment?
Donner la valeur de m.
Remarque: pour répondre à cette question
il faut rappeler que l' anion carbonate est une dibase faible.
Au contact de l' acide chlorhydrique l' anion carbonate
CO32- conduit dans un premier temps à l' anion
hydrogénocarbonate HCO3-. Puis l' anion hydrogénocarbonate
conduit au dioxyde de carbone dissous dans l' eau, CO2 aq, ou
"H2CO3", formule purement théorique de ce
que l' on pourrait appeler "acide carbonique".
Cela veut dire que le dioxyde de carbone est, par
conséquent, et réciproquement, un diacide faible, dont
les deux pKa, mesurés à 25°C, correspondent aux deux
couples acidobasiques précédents.
Couple dioxyde de carbone dissous / ion hydrogénocarbonate
CO2 aq / HCO3- : 6.4.
Couple hydrogénocarbonate / carbonate HCO3-
/ CO32- : 10.3.
Remarque: dans la question demandée, la seule partie
qui interviendra sera le passage de l' anion carbonate à l' anion
hydrogénocarbonate par action de l' acide chlorhydrique sur le carbonate
de sodium.
En effet la différence entre les deux pKa de l'
acide carbonique est telle qu' on dosera séparément la première
acidité de la seconde. Donc, réciproquement qu' on transformera
d' abord tout le carbonate en hydrogénocarbonate avant de transformer
(mais pas ici) l' hydrogénocarbonate en dioxyde de carbone
dissous dans l' eau.
La masse m de carbonate de sodium étant pesée à la balance de précision, confectionner, comme lors du TP précédent, la solution étalon, à l' aide de la fiole jaugée de 100 mL et de toute la verrerie nécessaire.
Calculer la concentration Cb de la solution étalon, en utilisant la masse m pesée, la masse molaire M du carbonate de disodium et le volume V de la fiole.
Calculer l' incertitude absolue DCb,
ainsi que l' incertitude relative![]() sur cette même concentration.
sur cette même concentration.
Présenter le résultat sous la forme suivante,
en précisant son unité:
Vérifier l' homogénéité des résultats quant aux chiffres significatifs et vérifier que l' incertitude relative est bien inférieure à 10%.
Partie 3: Etalonnage de la solution aqueuse d' acide chlorhydrique.
Procéder comme d' habitude.
Verser,à l' aide d' une pipette jaugée,
10 mL de solution étalon de carbonate de disodium dans un erlenmeyer.
Rajouter 20 mL d' eau distillée à l' aide d' une éprouvette.
Rajouter trois gouttes de phénolphtaléine.
Verser l' acide chlorhydrique contenu dans la burette,
goutte à goutte, jusqu' à décoloration de la phénolphtaléine.
Noter le volume Va d' acide versé à l'
équivalence.
Ecrire l' équation chimique du dosage, sachant que l' on passe du carbonate à l' hydrogénocarbonate, lorsqu' on fait réagir dans les conditions opératoires choisies, l' acide chlorhydrique avec le carbonate de disodium.
Calculer la concentration Ca de l' acide chlorhydrique. Vérifier qu' elle est très voisine, voire rigoureusement égale, à 0.200 mol.L-1.
Calculer l' incertitude absolue DCa,
puis l' incertitude relative ![]() sur la valeur calculée de Ca.
sur la valeur calculée de Ca.
Présenter le résultat final sous la forme
suivante, en précisant l' unité de Ca et en vérifiant
bien l' homogénéité des chiffres significatifs:
Partie 4: dosage de la solution de carbonate de (di)sodium.
Procéder comme d' habitude.
Prélever 10 mL de la solution aqueuse de carbonate
de disodium, portant le numéro de flacon 4, à l' aide
d' une pipette et verser dans un erlenmeyer.
Rajouter 20 mL d' eau distillée prélevée
à l' éprouvette.
Rajouter trois gouttes de phénolphtaléine.
Verser l' acide chlorhydrique jusqu' à décoloration de la phénolphtaléine.
Noter le volume équivalent V1. Ne pas remettre la burette à zéro.
Ecrire l' équation chimique qui a eu lieu, sachant que le carbonate de disodium a réagi avec l' acide chlorhydrique pour conduire , entre autres espèces présentes, à de l' hydrogénocarbonate de sodium. Nommer toutes les espèces qui se sont formées.
Rajouter alors trois gouttes d' hélianthine.
Verser l' acide chlorhydrique jusqu' à ce que
la solution contenue dans l' erlenmeyer devienne rouge orangé.
Noter le volume V2 d' acide chlorhydrique
rajouté en plus de V1.
Ecrire l' équation chimique qui a eu lieu, sachant
qu' il se forme du dioxyde de carbone dissous, entre autres espèces
chimiques. Nommer toutes les espèces chimiques qui se sont formées.
Quelle relation simple existe t-il entre V1 et V2? Est-ce normal?
Calculer la concentration Cb de la solution de carbonate
de disodium, à partir des résultats.
Attention! On ne fera pas intervenir dans le calcul le
rajout des 20 mL d' eau distillée dans l' erlenmeyer. Est-ce normal?
Calculer l' incertitude absolue DCb,
ainsi que l' incertitude relative ![]() sur le calcul de Cb précédent.
sur le calcul de Cb précédent.
Présenter le résultat sous la forme habituelle,
en précisant bien les unités de Cb et en tenant compte de
l' homogénéité des résultats quant aux chiffres
significatifs:
Partie 5: dosage d' une solution aqueuse de "soude carbonatée", à savoir un mélange d' hydroxyde de sodium et de carbonate de disodium.
On procèdera comme d' habitude.
Verser dans un erlenmeyer 10 mL de la solution à
doser, qu' on aura prélevée avec une pipette.
Rajouter 20 mL d' eau distillée à l' aide
d' une éprouvette.
Rajouter trois gouttes de phénolphtaléine.
Verser l' acide chlorhydrique jusqu' à décoloration
de la phénolphtaléine.
Noter le volume V3 versé. Ne pas remettre
à zéro la burette.
Ecrire de façon complète à chaque
fois (ions, molécules, espèces spectatrices...) les deux
équations chimiques qui sont intervenues.
La première équation concerne la neutralisation
de l' hydroxyde de sodium par l' acide chlorhydrique.
La seconde concerne la neutralisation du carbonate de
disodium en hydrogénocarbonate de sodium.
Remarque: comme le volume V3 ne permet pas de savoir quelle quantité d' acide chlorhydrique est venue réagir sur la soude et quelle quantité d' acide chlorhydrique est venue réagir sur le carbonate de disodium on est obligé de faire tomber un excès d' acide chlorhydrique dans le milieu.
Rajouter dans l' erlenmeyer trois gouttes d' hélanthine.
Verser l' acide chlorhydrique jusqu' à coloration
rouge orangé de la solution contenue dans l' erlenmeyer.
Noter l' excès de volume, V4, versé en plus du volume V3 précédent.
Ecrire de façon complète l' équation chimique du dosage, sachant que l' hydrogénocarbonate de sodium est transformé, entre autres, en dioxyde de carbone en solution aqueuse.
Calculer à partir des données les concentrations
Cb et Cb' de carbonate de disodium et d' hydroxyde de sodium.
Pour chacune de ces deux concentrations calculer les
incertitudes absolues DCb et DCb',
ainsi que les incertitudes relatives associées.
Remarque: on fera attention lors du calcul de l' une
des incertitudes, celui où interviendra le terme (V3-V4)
, à bien différentier le produit des facteurs. Voir le TP
précédent.
On présentera les résultats sous la forme
habituelle à chaque fois:
Retour au sommaire des TP de Chimie.
Retour sommaire des TP de Chimie.
Ce TP d' oxydoréduction se divise en deux parties.
Partie 1: étalonnage de la solution aqueuse de permanganate de potassium.
Partie 2: applications.
2.a. Dosage d' une solution aqueuse de sulfate de fer
(II).
2.b. Dosage d' une eau oxygénée.
2.c. Dosage en retour d' une solution aqueuse de dichromate
de potassium.
Partie 1: étalonnage de la solution aqueuse de permanganate de potassium.
Afin d' étalonner la solution aqueuse de permanganate de potassium on confectionnera une solution aqueuse d' acide oxalique.
On préparera 100 mL d' une solution aqueuse d'
acide oxalique de concentration Ca voisine de 0.075 mol.L-1.
Pour ce faire on la préparera à partir
de cristaux de formule (HO2C-CO2H, 2H2O),
de masse molaire 126.07 g.mol-1.
Remarque: cela veut dire que pour une mole d' acide oxalique cristallisée il y a deux moles d' eau qui sont enfermées dans le cristal. Cela ne veut pas dire que l' acide oxalique est "mouillé" quand on le touche mais qu' au niveau macroscopique il faudra tenir compte des molécules d' eau emprisonnées lors du calcul des masses de substance à peser.
On écrira l' équation chimique de la réaction
entre les ions permanganate et l' acide oxalique en milieu acide en utilisant
la règle mnémotechnique du gamma, ou toute autre méthode
fiable.
On décomposera l' équation chimique en
deux demi-équations redox: la demi-équation d' oxydation
et la demi-équation de réduction.
On mentionnera pour chacune d' elles le réducteur
et l' oxydant.
On écrira les demi-équations redox en faisant
d' abord intervenir, si nécessaire, les ions hydrogène H+,
et, ensuite, les ions hydronium, ou "oxonium", H3O+.
Remarque: pas plus l' une des écritures que l' autre ne rend compte de la "réalité" de la solvatation du proton en solution aqueuse, mais il faut bien "simplifier" et donner une écriture "commodément admise par tous".
On rappelle les deux couples redox qui sont mis en jeu
ici:
MnO4- / Mn2+ E°
= + 1.51 V/ ENH (électrode normale à hydrogène)
CO2 / HO2C-CO2H E°
= - 0.49 V/ ENH.
Manipulation.
Mettre la solution de permanganate de potassium dans la burette. Régler le zéro et chasser l' air contenu dans le bas de la burette. Défaire légèrement la vis arrière du robinet de la burette et laisser couler le liquide (attention à la couleur des doigts!!!) jusqu' à ce que la burette soit complètement remplie de liquide vers la partie inférieure. Resserrer la vis. La burette est prête.
Procéder classiquement.
Verser à l' aide d' une pipette 10 mL de la solution
étalon d' acide oxalique dans un erlenmeyer.
Rajouter à l' éprouvette (surtout ne pas
pipeter!!!!!) 20 mL de solution aqueuse d' acide sulfurique à 1
mol.L-1.
Faire couler environ 2 mL de solution de permanganate
de potassium dans l' erlenmeyer. Ne surtout pas remettre la burette à
zéro.
Chauffer sur la plaque chauffante en fond de salle de
TP l' erlenmeyer jusqu' à décoloration de la solution. La
solution prend progressivement des teintes allant du vieux rose au jaune
puis enfin devient incolore.
Revenir à la paillasse et poursuivre le dosage
jusqu' à coloration rose persistante.
Faire deux dosages à la goutte près.
Calculer la concentration COx de la solution
de permanganate de potassium.
Calculer l' incertitude absolue DCOx,
puis relative sur la mesure.
Présenter le résultat final sous la forme
habituelle:
Partie 2: applications.
Partie 2.a. Dosage d' une solution aqueuse de sulfate de fer (II).
Procéder classiquement.
Verser, à l' aide d' une pipette, 10 mL d' une
solution aqueuse de sulfate de fer (II) dans un erlenmeyer.
Rajouter, SUCCESSIVEMENT (car on verse l' acide sur l'
eau et surtout pas le contraire!!!), à l' éprouvette, 20
mL d' eau et 10 mL d' une solution aqueuse d' acide sulfurique à
1 mol.L-1 .
Faire deux dosages à la goutte près.
Ecrire l' équation chimique de la réaction entre les ions Fe (II) et les ions permanganate en milieu acide.
On rappellera les deux couples redox mis en jeu, ainsi
que les potentiels standard qui interviennent.
MnO4- / Mn2+ E°
= 1.51 V.
Fe3+ / Fe2+ E° = 0.68 V en
milieu H2SO4.
Calculer la concentration CRed de la solution de sulfate de fer (II) , l' incertitude absolue DCRed, ainsi que l' incertitude relative, associées à cette mesure.
Présenter le résultat sous la forme classique:
Partie 2.b. Dosage d' une eau oxygénée.
Procéder classiquement.
Prélever 10 mL de la solution aqueuse de peroxyde
de dihydrogène, alias "eau oxygénée", à l'
aide d' une pi....ette.
Rajouter 20 mL d' eau distillée, puis 10
mL de solution aqueuse d' acide sulfurique à 1 mol.L-1
dans l' erlenmeyer.
Faire deux dosages à la goutte près.
Ecrire l' équation chimique qui a lieu, sachant
que les deux couples redox qui interviennent sont, respectivement:
MnO4- / Mn2+ E°
= 1.51 V.
O2 / H2O2 E° = 0.69
V.
Calculer CRed et DCRed, puis présenter le résultat de la façon habituelle.
Partie 2.c. Dosage en retour d' une solution aqueuse de dichromate de potassium.
On s' arrange, dans ce type de dosage " en retour" ou
" par différence", à mettre un réactif en excès.
On connaît la quantité initiale de réactif
qu' on a mise. On dose ensuite l' excès de réactif.
Ainsi, par "différence" entre la quantité
initiale et la quantité résiduelle finale, on peut remonter
à la quantité de réactif qui a réagi avec une
espèce donnée.
Ce type de dosage, très courant en chimie, est utlisé ici dans la détermination de la concentration en dichromate de potassium contenu dans une solution aqueuse.
On procédera de façon classique, une fois encore.
Prélever à l' aide d' une pipette 10 mL
de la solution aqueuse de dichromate de potassium.
Rajouter à l' aide d' une pipette 10 mL de la
solution de sulfate de fer (II) utilisée lors de la partie 2.a.
Rajouter à l' aide de l' éprouvette 10
mL de solution aqueuse d' acide sulfurique à 1 mol.L-1
et 10 mL d' eau distillée.
Verser le permanganate de potassium jusqu' à persistance
de la coloration rose.
Faire deux dosages à la goutte près.
Les couples redox qui interviennent sont les suivants:
MnO4- / Mn2+ E°
= 1.51 V.
Cr2O72- /Cr3+
E° = 1.33 V.
Fe3+ / Fe2+ E° = 0.68 V.
Ecrire l' équation chimique de la réaction entre les ions Fe(II) et les ions dichromate.
Ecrire ensuite la réaction chimique entre les ions Fe(II) qui restent en excès et les ions permanganate.
Calculer pour le dichromate de potassium COx et DCOx. Attention le calcul de DCOx est TRES DUR!!!! (Rires!!!!).