Retour à l' index général du cours de chimie on line.
Ce cours se divise en cinq parties:
1.L' atome et ses modèles.
2.La
classification périodique des éléments.
3.La molécule vue selon LEWIS.
4.La théorie de l' hybridation.
5.La théorie des orbitales
moléculaires.
Première partie:
L' atome et ses modèles.
Plan du cours sur l' atome et ses modèles.
Retour au début du cours d' atomistique.
Retour à l' index général du cours on line.
I. Le foisonnement des idées scientifiques au début du XX° siècle.
1. Théorie de la relativité.
2. Effet photoélectrique.
3. Expérience de RUTHERFORD.
4. Spectre d' émission des atomes.
II. Le modèle atomique de Niels BOHR.
1. Expression du rayon Rn.
2. Expression de l' énergie En.
3. Les niveaux d' énergie
de l' atome d' hydrogène.
3.a. Série de LYMAN.
3.b. Série de BALMER.
3.c. Séries de PASCHEN, BRACKETT et PFUND.
4. Extension du modèle
de BOHR aux atomes hydrogénoïdes.
5. Calcul
de l' énergie d' ionisation de l' atome d' hydrogène et
d' un hydrogénoïde.
III. Les limites du modèle de BOHR.
1. Modèle de SOMMERFELD.
2. Modèle quantique de l' atome.
2.a. Association onde-particule. Louis de BROGLIE.
2.b. Equation de SCHRÖDINGER.
2.c. Conclusion
I. Le foisonnement des idées scientifiques au début du XX° siècle.
Retour au plan du cours sur l' atome et ses modèles.
I.1. Théorie de la relativité restreinte.
Les écrits d' Albert EINSTEIN (né en 1879 à Ulm, Allemagne, mort en 1955 à Princeton, Etats-Unis) datent de 1905, l' année de toutes les révolutions: première révolution russe en janvier 1905, fusillade du "9" (calendrier "julien") ou "22" (calendrier "grégorien"), janvier 1905 à Saint-Pétersbourg, mutinerie du cuirassé POTEMKINE en Mer Noire, séparation de l' Eglise et de l' Etat en France.....
Il n' avait alors que... 26 ans. Le talent n' attend pas forcément le nombre des années...
La mécanique dite "classique", datant de GALILEE,
de NEWTON, se trouvait incapable de décrire correctement les
objets se déplaçant à une vitesse proche de celle
de la lumière, dont EINSTEIN démontre qu' elle ne peut être
dépassée.
Masse et énergie sont reliées par une formule
condensée qui a fait le tour du monde:
E = m.c2
La masse m d' un objet n' est plus un invariant. Elle est reliée à la masse m 0, au repos, par la relation:
EINSTEIN a reçu le Prix NOBEL de Physique en 1921 pour ses travaux.
Voir ce lien sympa fait par un "jeune": La gravité, histoire des origines à nos jours.
EINSTEIN a quitté l' Allemagne en 1933, au moment
de la prise du Pouvoir par les nazis.
Durant la Seconde Guerre mondiale il prit une part
active dans le programme entamé par ROOSEVELT de construction de
la bombe atomique, dont la première tomba sur Hiroshima le 6 août
1945.
Après la Seconde Guerre mondiale, au moment
de la guerre froide, il a largement contribué à défendre
la Paix et à montrer que les savants ne sont pas forcément
responsables des utilisations qui sont faites par d' autres de leurs découvertes:
bref, sur un même registre, faut-il en vouloir aux Chinois
d' avoir inventé la poudre alors que cette dernière servait
pour faire, à l' origine, des.... feux d' artifice?
Questions de philosophie à méditer par
chacun d' entre nous....
I.2. Effet photoélectrique.
Cet effet a été découvert par le physicien allemand HERTZ ( cf les ondes "hertziennes") vers 1885.
On irradie par une lumière monochromatique, de fréquence n croissante, une plaque métallique reliée à un électromètre à cadran, déchargé à l' instant initial.
L' électromètre commence à se charger au-delà d' une fréquence n0. Les deux branches de l' électromètre s' écartent, signe de la présence d' électricité de même nature dans les plaques.
Que s' est-il passé?
Lorsqu' on éclaire une plaque métallique et qu' on procède à un balayage en fréquence pour la lumière on obtient une émission d' électrons à partir d' une fréquence-seuil n0 qui est caractéristique du métal utilisé. C' est EINSTEIN qui a apporté cette explication à l' expérience de HERTZ. Il s' était écoulé environ 20 ans entre les deux événements....
D' après EINSTEIN la lumière est porteuse de grains de matière, les "quanta", appelés aussi "photons", porteurs chacun d' une énergie W qui est égale au produit de deux termes: la constante de PLANCK et la fréquence de la radiation.
Ces grains d' énergie viennent, selon EINSTEIN, cogner contre les atomes métalliques de la plaque de l' électromètre et, s' ils ont suffisamment d' énergie, arrachent des électrons de la plaque, d' où la production d' électricité.
C' est ce qui constitue l' effet "photoélectrique", c' est à dire la production, grâce à la lumière, d' électricité.
Si l' on éclaire une plaque métallique avec une lumière monochromatique de fréquence n supérieure à la fréquence-seuil n0, le surcroît d' énergie par rapport au travail d' extraction W0, tel que:
L' effet photoélectrique est très utilisé dans les systèmes d' alarme qui équipent bon nombre d' établissements en contact avec le public. Le passage d' une personne là "où il ne faut pas" déclenche toutes les alarmes....
Là aussi, cette expérience, son explication, ont provoqué une véritable révolution: jusqu' alors la lumière avait été décrite comme un phénomène de nature "ondulatoire": durant tout le XIX° siècle, de FRESNEL à YOUNG, la lumière était considérée comme un système d' ondes.
Il apparaît alors que la lumière est aussi "corpusculaire", c' est à dire composée de "grains".
C' est cet aspect corpusculaire qui a permis de comprendre ultérieurement l' effet COMPTON, par exemple.
On parle alors pour la lumière d' aspect "dual", de "dualité onde-corpuscule": deux choses en une même chose.
Pour l' heure les physisciens n' ont pas réussi
à expliquer par une seule même théorie ce qu' est la
lumière.
Selon les besoins on privilégie l' aspect "ondulatoire"
de la lumière, et selon d' autres moments, on privilégie
plutôt l' aspect "corpusculaire".
Il y a encore du pain sur la planche....
I.3. Expérience de RUTHERFORD.
La mise en évidence des électrons a été faite à la fin du XIX° siècle: expérience de THOMSON, tube cathodique de CROOKES.
Il restait à élucider la structure de l' atome dont l' existence n' était plus remise en question à cette époque.
Vers 1908 RUTHERFORD expliquait une expérience réalisée précédemment qui se révéla fondamentale.
Remarque préliminaire: il faut savoir que la découverte de la radioactivité naturelle par Henri BECQUEREL, Pierre et Marie CURIE en 1898, avait déjà permis de se procurer des particules alpha, c' est à dire des ions He2+, à partir de matériaux divers.
Lorsqu' on bombarde une feuille d' or, d' épaisseur
voisine du micromètre, par une source émettrice de particules
alpha, on constate que la majorité des particules passe à
travers la feuille.
Toutefois, il n' en demeure pas moins que certaines particules
sont violemment déviées et retournent du côté
de la source.
A partir de ces deux constatations, deux conclusions ont
été tirées:
1. L' atome est essentiellement constitué de vide:
d' où le fort taux de passage des particules alpha à travers
la feuille d' or.
2. L' atome, électriquement neutre, est constitué
d' une partie chargée positivement, qui est très petite:
c' est ce qui explique la répulsion forte, quoique rare au plan
statistique, des particules alpha, de même nature électrique
que le "noyau".
Ainsi donc, il y a dans l' atome un "noyau", positif, tout petit, autour duqsuel gravite un nuage négatif, constitué d' électrons.
Reste désormais à élucider comment tournent ces électrons autour du noyau....
I.4. Spectre d' émission des atomes.
Indépendamment de ces expériences on avait
mis en évidence à cette époque le spectre d' émission
de certains atomes d' éléments chimiques.
C' était le cas notamment pour l' hydrogène.
Quand on excite, sous une forte différence de potentiel, des molécules de dihydrogène on peut obtenir une quantité appréciable d' atomes d' hydrogène excités et collecter, puis analyser, la lumière émise à l' aide d' un élément dispersif comme un prisme ou un réseau.
On constate alors, de même que pour d' autres éléments chimiques, qu' on obtient un spectre cannelé de raies, ce qu' on appelle un spectre "discret", et non pas un spectre continu, comme celui émis par la lumière solaire.
Pourquoi l' hydrogène émet-il un spectre "discret" de lumière?
Niels BOHR allait permettre de comprendre cet aspect discontinu des propriétés de la matière.
Retour au plan du cours sur l' aome et ses modèles.
II. Le modèle atomique selon Niels BOHR (1913).
Retour au plan du cours sur l' atome et ses modèles.
L' idée de Niels BOHR (physicien danois né en 1887), et qui ne fut pas contestée au début, était la suivante: l' atome, avec son noyau et ses électrons, doit tout siumplement être un "système solaire miniature": le noyau figurant le Soleil et les électrons les planètes qui gravitent autour.
II.1. Expression du rayon Rn de l' atome d'
hydrogène, dans la théorie de BOHR.
L' électron est soumis, dans ce modèle,
à deux forces extérieures: son poids Pet
la force de COULOMB, F.
Le poids P est
négligeable devant la force coulombienne (cf cours de physique de
1ère S).
La force de COULOMB a pour expression:
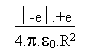
Or, dans le cas d' un mouvement circulaire uniforme, ce
qui est postulé ici, l' accélération tangentielle
est nulle. L' accélération a
se confond alors avec l' accélération normale.
Avec alors:
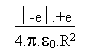 =
= A partir de là BOHR postule que le moment cinétique s de l' électron est un multiple entier de la constante de PLANCK réduite:
L' égalité écrite en (2) constitue un trait de génie. BOHR, en effet, fait un lien alors entre l' Ancien (le moment cinétique exprimé dans le cadre de la mécanique classique) et le Moderne (la quantification des propriétés de la matière).
A partir de là, le reste n' est plus que "tripatouillage" de données.
On va s' arranger pour faire disparaître v et on isolera R qu' on exprimera en fonction des données.
m.v2 = 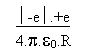 (3)
(3)
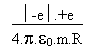 (4)
(4)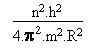 (6)
(6)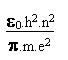 (7)
(7)On appelle n le "nombre quantique principal". C' est un entier naturel, non nul.
II.2. Expression de l' énergie En de
l' atome d' hydrogène.
Un des acquis fondamentaux de la mécanique classique
a été d' énoncer le fait que l' énergie totale
E d' un système mécanique est égale à
la somme de deux termes, l' énergie cinétique Ec
et l' énergie potentielle Ep.
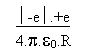
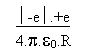 (10)
(10)Tout se passe comme si un opérateur imaginaire
venait tirer sur l' électron, en orbite autour du noyau, dans la
même direction que la force coulombienne, MAIS dans un sens opposé.
Cet opérateur imaginaire amènerait alors l' électron
de la distance R à la distance plus l' infini.
Le travail W effectué par la force exercée
par cet opérateur imaginaire serait donné par l' intégrale
suivante:
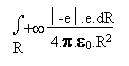 (11)
(11)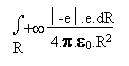 (12)
(12)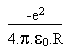 (13)
(13)En réunissant les résultats de (10) et (13) on arrive à l' énergie totale du système:
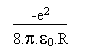 (14)
(14)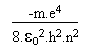 (15)
(15)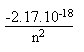 J
(16)
J
(16)II.3. Les niveaux d' énergie de l' atome d' hydrogène.
Retour au plan du cours sur l' atome et ses modèles.
A partir de la formule (17) on positionne les niveaux
d' énergie de l' atome d' hydrogène.
On fait varier n de la valeur n = 1 (état fondamental)
à n = infini, état ionisé.
C' est un excellent exercice à faire sur feuille
de papier millimétré.
Prendre la feuille dans le sens vertical.
Graduer la feuille en mettant l' origine de l' énergie,
correspondant à E = 0, tout à fait en haut.
Prendre comme unité 0.5 eV égale 1 cm.
Positionner les différents niveaux.
Bien entendu vers 0 tous les niveaux se rapprochent.
N' en dessiner que quelque uns pour que ça ne fasse pas "nuage noir".
On remarque que les niveaux énergétiques ne sont pas équidistants.
Le niveau correspondant à n = 1 est le seul niveau qui soit l' état fondamental du système.
Tous les autres niveaux sont des niveaux excités.
Le premier état excité correspond donc au niveau pour lequel n = 2.
II.3.a. Série de LYMAN.
A partir du positionnement des différents niveaux d' énergie on peut expliquer pourquoi il y a émission de raies.
L' atome d' hydrogène peut absorber certaines valeurs
d' énergie et passer dans un état excité.
Il peut alors céder cette énergie emmagasinée
sous la forme d' un photon lumineux dont l' énergie E , égale
à h.n,
sera égale à la différence E p - E n
des niveaux d' énergie associés, si l' électron est
passé d' un niveau p à un niveau n, moins excité.
On aura alors:
Il faut toujours avoir en mémoire que DE est toujours positif. Cela permet d' éviter des "ennuis" lors de la manipulation de ces formules.
Retenir que pour qu' il y ait émission d' un photon il faut toujours passer d' un niveau excité vers un niveau MOINS excité, donc "descendre" de "p" à "n".
A partir de là c' est un jeu d' enfant que de trouver ce que c' est que la série de LYMAN.
La série de LYMAN correspond à toutes les transitions des états excités de l' atome d' hydrogène vers l' état fondamental.
Dans (18) il faut remplacer n par la valeur 1.
On arrive alors à:
On peut exprimer la série de LYMAN en une série de fréquences ni , qu' on trouve à partir de (19).
On peut aussi l' exprimer en une série de longueurs
d' onde li.
On se remémorera la relation suivante, liant la
fréquence d' une radiation à sa longueur d' onde et à
c, en l' occurence la vitesse de la lumière:
On peut aussi exprimer la série de LYMAN en nombre
d' onde, noté n.
On définit le nombre d' onde par le rapport suivant:
On aura alors:
Usuellement, en spectroscopie on utilise comme unité de nombre d' onde le cm-1.
Remarque: la quantité ![]() est
appelée constante de RYDBERG. On la note souvent R H.
est
appelée constante de RYDBERG. On la note souvent R H.
Sa valeur est égale à 1.09.107 m-1,
ou, pour arrondir et s' exprimer en cm-1, 110 000 cm-1.
C' est une valeur qui est à retenir.
Le modèle de BOHR a permis la mesure de la constante de RYDBERG.
Pour la série de LYMAN on notera sous forme de
tableau les résultats des longueurs d' onde li
, exprimées en nanomètres, pour les transitions principales:
| Longueur d' onde pour la transition | Valeur en nm |
| De 2 vers 1 | 122 |
| De 3 vers 1 | 102 |
| De 4 vers 1 | 97 |
| De 5 vers 1 | 95 |
| De l' infini vers 1 | 91 |
On remarquera que les valeurs de ces longueurs d' onde se situent dans la zone ultra-violette du spectre des radiations lumineuses.
II.3.b. Série de BALMER.
C' est la série voisine de la série de LYMAN.
Elle correspond à toutes les transitions relatives
au retour sur le niveau n = 2, le premier état excité de
l' atome d' hydrogène.
Nous aurons alors, pour les nombres d' onde, par exemple:
Si l' on récapitule les résultats sous forme
de tableau, tout comme pour la série de LYMAN, on arrive à:
| Longueur d' onde pour la transition | Valeur en nm |
| De 3 vers 2 | 658 |
| De 4 vers 2 | 488 |
| De 5 vers 2 | 435 |
| De 6 vers 2 | 411 |
| De l' infini vers 2 | 365 |
Les transitions de la série de BALMER se situent
toutes dans le visible, sauf la dernière (de l' infini vers n =
2), qui est dans le proche ultra-violet.
II.3.c. Séries de PASCHEN, BRACKETT et PFUND.
Ce sont les séries homologues, supérieures.
Pour la série de PASCHEN on aura un ensemble de transitions correspondant au retour sur le second niveau excité, à savoir le niveau pour lequel n = 3.
On aura, pour les nombres d' onde, la relation suivante:
On aura, pour les nombres d' onde, la relation suivante:
On aura, pour les nombres d' onde, la relation suivante:
Ces trois séries se situent dans le domaine infra-rouge du spectre lumineux.
Retour au plan du cours sur l' atome et ses modèles.
II.4. Extension du modèle de BOHR aux atomes hydrogénoïdes.
Retour au plan du cours sur l' atome et ses modèles.
On appelle "hydrogénoïde" une espèce chimique qui comporte un noyau atomique avec Z protons, un seul électron gravitant autour du noyau.
Par exemple l' hydrogénoïde de l' uranium, de numéro atomique 92, serait l' ion U 91+. Inutile de dire que cet ion ne court pas les rues.....
Remarque: le nombre de neutrons n' intervient pas, si j' ose dire, dans ce modèle, vu que le neutron n' a été découvert qu' en 1932 par CHADWICK et qu' il est... neutre électriquement.
En reprenant les équations pour l' atome d' hydrogène ( Z = 1), on remplace certaines expressions en tenant compte du fait que Z est différent de 1 dans le cas des hydrogénoïdes.
La force de COULOMB F s' écrit dès lors:
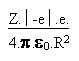 (28)
(28)En remplaçant dans les équations (1), (2), (3), (4), (5), (6), (7) la force de COULOMB par son expression en (28), on arrive, tous calculs faits, à:
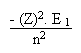 (30)
(30)Retour au plan du cours sur l' atome et ses modèles.
II.5. Calcul de l' énergie d' ionisation de l' atome d' hydrogène et d' un hydrogénoïde.
Retour au plan du cours sur l' atome et ses modèles.
L' énergie d' ionisation E.I. correspond à l' énergie qu' il faut fournir pour arracher un électron et le porter à l' infini.
Pour l' atome d' hydrogène E.I. correspond à l' énergie qu' il faut apporter à l' atome d' hydrogène lors de la réaction chimique suivante:
En appliquant la relation (19) et en remplaçant p par "plus l' infini" on arrive à:
DE = E.I. = + E 1
DE = E.I. = + 13.6 eV (31)
On insistera LOURDEMENT sur le signe "plus".
Pour l' hydrogénoïde de l' uranium (Z = 92) E.I. correspondrait à l' énergie à mettre en jeu lors de la réaction chimique, tout hypothétique:
Remarque importante: la méthode de BOHR ne permet
pas, pour un atome quelconque, de calculer l' énergie de la énième
ionisation.
Elle ne marche que lorsqu' on veut passer d' un seul
électron périphérique, quelle que soit la charge Z
du noyau, à plus du tout d' électron.
Par exemple, dans le cas de l' atome d' hélium
He (Z = 2), la méthode de BOHR permet seulement de calculer
l' énergie de seconde ionisation de l' atome d' hélium, bref,
l' énergie à mettre en jeu pour passer de He+
à He2+.
Pour l' énergie de première ionisation,
bref pour passer de He à He+, étant donné
qu' il y a deux électrons qui gravitent autour de l' atome d' hélium,
la méthode de BOHR n' est pas applicable.
Pour l' atome de lithium (Z = 3), la méthode de BOHR permet juste de calculer l' énergie de troisième ionisation, bref l' énergie qu' il faut mettre en oeuvre pour passer de Li 2+ à Li 3+.
Retour au plan du cours sur l' atome et ses modèles.
III. Les limites du modèle de BOHR.
Retour au plan du cours sur l' atome et ses modèles.
L' accueil de la théorie de BOHR en 1913 fut extraordinaire:
qui plus est elle émanait de quelqu' un de jeune (il avait alors
26 ans).... ce qui rendait la Science à tout le moins sympathique....
On pensait vraiment avoir fait le tour de la question
de la structure de l' atome et on était émerveillé
par le fait d' imaginer cette "homothétie" en quelque sorte entre
le monde macroscopique (le système solaire) et le monde microscopique
constitué par l' atome.
Hélas, trois fois hélas, les premiers craquèlements intervinrent avec l' atome d' hélium, bref lorsqu' on avait, non plus un mais deux électrons tournant autour du noyau.
Dans sa théorie BOHR n' avait nullement tenu compte des répulsions interélectroniques: dans le cas de l' atome d' hydrogène bien évidemment il n' y en a pas. Dans le cas de l' atome d' hélium oui.
BOHR ne pouvait pas non plus rendre compte, par ses résultats de 1913, du dédoublement de certaines raies spectrales sous l' effet d' un champ magnétique: c' est ce que l' on appelle l' effet ZEEMAN.
il fallait donc TROUVER AUTRE CHOSE....
Niels BOHR a été Prix Nobel de Physique en 1922, juste un an après Albert EINSTEIN.
III.1. Le modèle de SOMMERFELD.
Le physicien SOMMERFELD, devant les incohérences de la modélisation de BOHR a alors entrepris de remplacer les trajectoires de l' électron, postulées circulaires par BOHR, en trajectoires elliptiques, tout comme la Terre tourne de façon elliptique autour du Soleil.
Malgré cette tentative, le modèle a échoué. De nouvelles incohérences ne manquant pas d' apparaître....
III.2. Le modèle quantique de l' atome.
Après la rupture brutale pour toute activité
scientifique durant la Première Guerre mondiale, les travaux sur
la structure de l' atome reprirent de plus belle et tous azimuts.
III.2.a. L' association onde-particule de Louis de BROGLIE.
Ce physicien français, né en 1892, émit en 1924 l' hypothèse selon laquelle à chaque particule en mouvement serait associée une onde l, telle que :
Cette hypothèse jeta les bases de la nouvelle mécanique, dite mécanique ondulatoire, qui allait permettre de mieux décrire l' atome comme entité microscopique qui n' obéit pas aux mêmes lois que l' infiniment grand.
On se rend compte que si l' on pose que n.l,avec l égal à la longueur d' onde de De BROGLIE, est égal à la circonférence de la trajectoire circulaire de l' électron dans le modèle de BOHR, bref qu' on suppose qu' on crée un système d' ondes stationnaires autour du noyau de l' atome d' hydrogène, soit :
Louis de BROGLIE a été Prix Nobel de Physique en 1929 pour ses travaux.
III.2.b. L' équation de SCHRÖDINGER.
Vers la même époque, les années 20, le physicien autrichien Erwin SCHRÖDINGER posa son équation , demeurée célèbre, afin de décrire la mécanique de l' atome d' hydrogène.
En mécanique classique on a vu que l' énergie
d' un système mécanique est égale à la somme
de deux termes, l' énergie cinétique et l' énergie
potentielle.
Ces grandeurs sont toutes des "scalaires", c' est à
dire des nombres.
En mécanique "quantique" ou "ondulatoire" , c'
est à dire en mécanique de l' infiniment petit, l' énergie
totale, l' énergie cinétique et l' énergie potentielle
ne sont plus des scalaires mais deviennent ces "opérateurs".
Bref, plus question alors de donner une valeur unique
pour ces termes.
On introduit alors un outil, purement artificiel, une
fonction mathématique, en général notée Y,
qui
dépend des coordonnées d' espace et de temps: x, y, z et
t.
Cette fonction, appelée "fonction d' onde", est
telle que lorsqu' on l' applique à l' équation:
Energie totale = Energie cinétique + Energie potentielle
Pour simplifier on constate que le produit:
A.Y" + B.Y = Energie totale.Y (33)
On constate que le terme A, faisant intervenir la dérivée seconde de la fonction Y, est le terme représentatif de l' énergie cinétique du système, et que le terme B est représentatif de l' énergie potentielle du système.
Cette équation n' admet de solution exacte que
pour l' atome d' hydrogène et les ions hydrogénoïdes,
en raison de l' absence de répulsion interélectronique, vu
qu' il n' y a qu' un seul électron qui gravite autour du noyau.
Pour les autres atomes, les atomes "polyélectroniques"
elle n' admet que des solutions approchées, calculées en
minimisant les répulsions interélectroniques.
Je vais donner un peu plus loin dans le cours (cliquer ici) la solution exacte de l' équation de SCHRÖDINGER pour les premiers niveaux énergétiques de l' atome d' hydrogène ou d' un ion hydrogénoïde.
Ce qu' il y a de remarquable c' est qu' elle induit, de par ses solutions, des zones où l' électron aura une forte probabilité de présence, qui seront totalement différentes des fameuses trajectoires circulaires établies par BOHR.
On parlera alors d' orbitales, qu' on étudiera plus avant dans la seconde partie du cours, celle relative à la classification périodique des éléments.
Ici on n' est pas dans le domaine des certitudes mais on entre, en mécanique quantique, dans le domaine des probabilités de présence.
Ce qui est remarquable, mais peut-être l' est-ce autant pourle modèle de BOHR, c' est qu' on retrouve, pour l' atome d' hydrogène, les valeurs calculées par BOHR au niveau de l' énergie: le fameux -13.6 eV, etc...
III.2.c. Conclusion.
Alors BOHR ringard? Vilain? Il a fait "faux" et on apprend ses théories? Mais que fait la police?
Oui, BOHR a fait "faux", du moins partiellement.
Oui, il n' y a pas en réalité de trajectoire pour l' électron en mécanique quantique: il n' y a juste que des probabilités de présence de l' électron dans des zones plus ou moins complexes...
Oui, il n' a pas prédit les spectres d' émission des atomes polyélectroniques, pas plus qu' il n' a pu rendre compte de l' effet ZEEMAN....
Mais bon......
En 1913, quand il a postulé sa théorie, qu' y avait-il à la place? Rien. La réponse est RIEN.
Alors il aura pris le risque de se tromper.
C' est très important.
En Sciences qui ne prend pas le risque de se tromper
perd la possibilité majeure d' évoluer.
Une Science est toujours évolutive et BOHR aura
été l' exemple de celui qui, à partir de rien, aura
créé une théorie et l' aura soumise à l' épreuve
de la pratique.
Si la pratique infirme la théorie eh bien il ne
faut pas en vouloir à la pratique mais revoir sa théorie.
C' est ce qu' il aura fait, et il aura laissé ici la place aux autres,
en l' occurence, pour y parvenir.
En ce sens le modèle de BOHR, tout périmé
soit-il, est un exemple, je dirais majeur, dans l' appréhension
des Sciences par quelqu' un qui s' y frotte.
Un bel exemple de formation....