II.3. Les pH des solutions aqueuses simples.

 Retour au plan du cours sur les pH des solutions aqueuses.
 

II.3.a. Cas d'un monoacide fort.

 Retour au plan du cours sur les pH des solutions aqueuses.

On prendra le cas du chlorure d'hydrogèneHCl dissous dans l'eau: la solution d' acide chlorhydrique.
On a la réaction:           H₂O  +  HCl   H₃O⁺  + Cl^-.
On  écrira alors deux relations qu'on retrouvera SYSTEMATIQUEMENT dans TOUT CALCUL DE pH.

Il s'agit premièrement de l'équation de  conservation de la masse, de conservation de la matière pour l'espèce considérée.

On aura, dans le cas de l'acide chlorhydrique :
C_{acide chlorhydrique global}= (HCl)_{non dissocié}  + (HCl)_dissocié.
Or, (HCl)_{non dissocié} vaut 0, puisque HCl est un acide fort. Et (Cl^-) vaut alors C₀mol.L^-1.

Il s'agit deuxièmement de l'équation de conservation de la charge, appelée aussi "bilan électrique" ou , le plus souvent, "électroneutralité".

Ici on aura: (H₃O⁺) =   (Cl^-)  +  (HO^-)

On adoptera, dès lors, dans toute la suite du cours, la convention d'écriture beaucoup plus légère qui est:
     h   =  (H₃O⁺)   w  =  (HO^-)
On  peut tout de suite négligerwdevant h, vu qu'on a toutes les raisons à s'attendre à ce que le pH d'un acide soit... acide.
On arrive donc à       (H₃O⁺) @C₀, d'où pH = - logh  = -logC₀.

Cette formule  a un domaine de validité tant que la concentration C₀ est supérieure ou égale à 10^-6mol.L^-1.

Si la concentration C₀ a une valeur inférieure à 10^-6 mol.L^-1. Que se passe t-il alors?

C'est un cas qui n'est, je dirais, qu'académique. C'est une question "piège" à certains oraux de concours, à certains écrits, pour tester la sagacité de l'étudiant, mais cette question n'a que cet "intérêt".
En effet, je me permets cette réflexion "iconoclaste" car faire des dilutions aussi fortes dans une eau qui, la plupart du temps n'est pas à pH 7 du fait de la présence de dioxyde de carbone dissous, et chercher une variation très infime par rapport à la "neutralité" c'est vraiment pas "tenable". C'est l'expérimentateur qui parle.

Revenons à l'exemple académique.
Il faut alors résoudre en tenant compte des ions de l'eau, bref, de l'équilibre d'autoprotolyse de l'eau.

On demande par exemple le pH d'une solution d'acide chlorhydrique à 10^-8mol.L^-1.
Si l'on est trop "pressé" on peut se jeter dans la gueule du "loup" et répondre:"Le pH vaut -log10^-8 , soit.... 8!!!! "

Enfer et damnation!!!!! Le pH d'un acide est tout d'un coup ... basique!!!!

What happened? Qué paso?

On écrit la conservation de la matière:
10^-8 mol.L^-1= (Cl^-)  +  (HCl)_{non dissocié}

(HCl)_{non dissocié}  vaut 0 mol.L^-1.
On écrit l'électroneutralité de la solution:

On en tire facilement  w . On a     w  = . D'où l'équation du second degré suivante:

Quand je vous disais que ce pH est "académique".....

A titre d'exercice on peut chercher le pH d'une solution d'acide chlorhydrique à 10^-7mol.L^-1.

 Retour au plan du cours sur les pH des solutions aqueuses.

II. 3.b. Cas d'une monobase forte.

 Retour au plan du cours sur les pH des solutions aqueuses.

On prendra le cas de l'hydroxyde de sodium, de formule NaOH, qu'on  dissoudra à raison de C₀mol.L^-1.
On a la réaction de dissolution dans l'eau  suivante:
                                                     NaOH   Na⁺  +  HO^-
Comme la mise en solution conduit à ce que la réaction précédente soit totale, on se retrouve alors avec  w  qui vaut C₀ mol.L^-1.
Or, on a h qui vaut:  . En remplaçant w par C₀ on arrive alors, très facilement, en prenant le logarithme de l'expression, à:

On retrouve un raisonnement symétrique à celui évoqué lors de la question "académique" du pH d'une solution d'acide chlorhydrique à 10^-8 mol.L^-1.

Si l'on considère le calcul du pH d'une solution d' hydroxyde de sodium à 10^-8 mol.L^-1 et que l'on élimine la solution pH = 6  que donnerait une utilisation  peu "raisonnable " de pH = 14 + logC₀, on arrive alors à l'équation d'électroneutralité suivante :  (Na⁺) + h  = w = .
On a (Na⁺) qui vaut C₀, soit 10^-8 mol.L^-1.
On résout l'équation du second degré en h qui a la forme suivante:

 Retour au plan du cours sur les pH des solutions aqueuses.

II.3.c. Cas d'un monoacide faible.

 Retour au plan du cours sur les pH des solutions aqueuses.

On prendra l'exemple de l'acide acétique, alias éthanoïque, de formule CH₃CO₂H, abrégé en "AcOH", où le radical "Ac" désigne le radical "éthanoyle" alias "acétyle", de formule "CH₃CO-".
C'est là une abréviationque l'on rencontre très souvent dans les ouvrages anglo-saxons, et qui a la commodité d'être dactylographiée aisément.
L'anion conjugué de l'acide acétique sera l'anion "acétate" , alias "éthanoate", de formule CH₃CO₂^-, abrégé en "AcO^-".
Le pK_a du couple acide acétique  / anion acétate vaut 4.75 à 25 °C.
On  se placera dans le cas le plus intéressant qui est celui où la concentration C₀de l'acide acétique est ³ 10^-6mol.L^-1.

On écrira l'équation chimique qui a lieu:

CH₃CO₂H  +  H₂O H₃O⁺  + CH₃CO₂^-.

AcOH  + H₂O H₃O⁺  +  AcO^-.

 2H₂O H₃O⁺  +  HO^-.

Or, du fait de la simplification dans l'électroneutralité, K_a devient égale à: .

On peut encore vérifier a posteriori que  les ions hydronium H₃O⁺provenant de l'eau étaient négligeables devant ceux apportés par l'acide acétique lui même mis en solution. En effet, d'un côté nous avons 1.32.10^-3 mol.L^-1 et de l'autre nous avons quelque chose comme 10^-7mol.L^-1.

D'autre part, si nous recherchons la "réaction prépondérante" nous retrouvons bien qu'elle est celle relative à la dissociation de l'acide acétique. La valeur de la constante d'équilibre vaut 10^-4.75, elle est beaucoup plus grande que 10^-14.
D'autre part, en s'intéressant au bilan de matière produit par la réaction censée être prépondérante on voit bien que 1.325.10^-3 mol est beaucoup plus grand que 10^-7mol, ces 10^-7 mol devenant, du coup,  négligeables.

J'ouvre à nouveau une parenthèse de taille, qui a son "importance", si j'ose dire, avec la question du "diagramme des espèces dissoutes".

La connaissance de ce diagramme permettra éventuellement de faire des "simplifications" dans les calculs. Il existe en effet des "formules approchées" de calcul de pH.
Je n'en ressens pas forcément l'utilité en toutes circonstances car j'estime que la résolution d'une équation du second degré est bien "facile" et surtout très souvent "suffisante" pour mener à bien tout calcul de pH. Je donne malgré tout la "méthode" des formules approchées pour les "inconditionnels".

Il faut donc tracer ici, en fonction du pH (la variable) , de pK_a  (le paramètre) et de C₀, l'évolution des concentrations respectives des formes moléculaire AcOH et ioniséeAcO^- des espèces dissoutes de l'acide acétique.
On a la constante d'acidité K_a du  couple acide acétique / ion acétate qui s'écrit :.
On écrit l'équation de conservation de la matière :
                                              C₀ =  (AcOH)  +  (AcO^-)
On peut écrire l'électroneutralité si on veut mais ici ça ne nous servira à rien.
De l'expression précédente de K_a on tire (AcOH).
On a (AcOH) qui vaut: 
A partir de là on écrit la "trivialité" suivante:

(AcOH)  +  (AcO^-) = (AcO^-). (1  +)

Et comme (AcOH) est égal à , du fait de l'expression de K_a, on arrive en multipliant  par  à:

(AcOH) = 

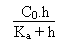
On peut les réarranger, voire les exprimer d'une façon encore plus générale.
On réintroduit la notion de degré de dissociation a: a sera égal à : 
En introduisant  a  on s'affranchit de la concentration C₀.
On exprime K_a et h sous une forme exponentielle:
On a  K_a = 10^-pKa et  h  =  10^-pH.
Les deux expressions de (AcO^-) et de (AcOH), devenues dès lors, respectivement, a et 100-a  deviennent dès lors:
Pour a, relatif à l'évolution au cours de la variation (tout à fait éventuelle, provoquée si besoin par l'expérimentateur) du pH  de la formeAcO^-: .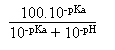
Pour 100 - a, relatif à l'évolution  (tout à fait éventuelle, provoquée si besoin par l'expérimentateur)au cours de la variation du pH de la forme AcOH:.
On peut, dès lors, tracer l'allure des deux fonctions mathématiques décrivant l'évolution des formes AcOH et AcO^- dans le milieu.
On devine aisément que si le pH augmente la forme AcOH régressera et qu'aucontraire la forme AcO^-augmentera.

On obtient le graphe suivant: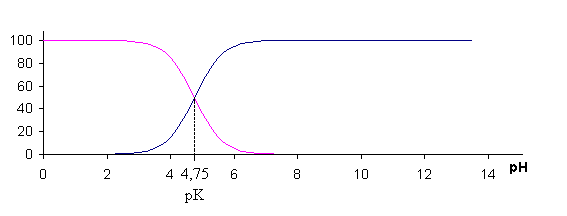
On voit que les deux fonctions se croisent pour la valeur de pH égale à pKa du couple acidobasiqueAcOH / AcO^- . La valeur de l'ordonnée à l'intersection est de 50%.
On voit sur le graphe que si le pH de la solution est inférieur à pK_a-1 alors c'est la forme AcOH qui estmajoritaire: elle représente de 90 à 100% du total.
En revanche, si le pH de la solution est supérieur à pK_a + 1, alors c'est la forme AcO^-  qui est majoritaire et qui représente de 90 à 100% du total.
Ce sont les deux intervalles de pH  extrêmes.
Entre les valeurs pK_a-1 et  pK_a +1 , il y a des quantités non négligeables de l'unedes formes par rapport à l'autre.

A partir de ces considérations sur les proportions respectives des deux formes acidobasiques présentes dans la solution on peut envisager l'application éventuelle des formules approchées.

On se rappelle qu'on avait comme expression abrégée de la constante d'acidité K_a, une fois que dans l'électroneutralité on négligeait les ions hydroxyde de l'eau:
Ka  = .
A partir de là on voit que si C₀est très supérieure à h, alors le dénominateur se simplifie et l'on ne  retrouve plus que C₀à ce même dénominateur.
Quand est-ce qu'on peut avoir C₀ qui est très supérieure à h?
Du fait que h est égal à (AcO^-), c'est lorsqu'on se situe sur le diagramme de prédominance à gauche de la valeur pK_a-1. A ce moment là on a (AcOH) qui représente au moins 90% du total de C₀ et on peut considérer, dès lors, comme négligeable devant C₀ la valeur de (AcO^-), donc celle de h.
On arrive alors à: K_a = .
A partir de là c'est un jeu d'enfant que de prendre le logarithme décimal de la formule et que d'arriver à l'expression simple:

C'est "LA"  formule "approchée", la "fameuse"  formule approchée du pH des monoacides faibles en solution aqueuse.

Quel est son "domaine de validité"?

Il faut pour pouvoir l'appliquer que le pHtrouvé à l'aide de cette formule soit strictement inférieur à la valeur de pK_a-1.

Si jamais la valeur trouvée par cette formule est supérieure à la valeur de pKa1 alors il faut  résoudre le trinôme, l'équation du second degré en h si vous préférez, obtenu à partir de l'expression de K_a suivante:

K_a  = 

Le cas où "ça marche".

Quel est le pH d'une solution aqueuse d'acide éthanoïque de concentration 0.1 mol.L^-1 sachant qu'on donne pour valeur de pK_a du couple acidobasque AcOH /AcO^-la valeur de  4.75 à 25°C?

On applique la formule approchée et on a:

Cette valeur est-elle "plausible"?

Si l'acide avait été "fort" on aurait trouvé pH =1.

Ici il est "faible" donc c'est "normal" de trouver une valeur plus grande que 1.
La formule approchée a donné un pH qui est strictement inférieur à 3.75, c'est à dire à la valeur numérique de pK_a-1, doncon pouvait bien l'appliquer.
Le résultat, à défaut peut-être d'être "juste" est en tout cas plausible et l'on peut le donner sans "rougir" si j'ose dire.

Le cas où "ça ne marche pas".

Quel est le pH d'une solution aqueuse d'acide éthanoïque, de concentration C₀égale à 10^-5 mol.L^-1, sachant que le pK_a vaut, etc.........

On applique la formule approchée.
On pose la calcul suivant:

K_a = 

En conclusion: il ne faut pas oublier "complètement" si l'on veut les formules approchées mais en tout cas mieux vaut s'en méfier. La résolution de l'équation du second degré est, quant à elle, imparable... sauf erreurs de... calcul!

Evoquons, pour conclure ce paragraphe, le cas du pH d'un monoacide faible de concentration C₀inférieure à 10^-6 mol.L^-1.

On voit là aussi que si l'acide avait été "fort" le pH aurait valu 6 au minimum. Le maximum étant bien entendu légèrement inférieur à 7.
Ici, comme l'acide est faible on aura un pH qui sera supérieur à 6 mais inférieur à  la valeur 7.

Si l'on examine le cas de l'acide éthanoïque, on voit sur son diagramme de prédominance que  pour l'intervalle de pH  compris ente les valeurs 6 et 7 c'est la forme ionisée AcO^- qui est largement majoritaire.  Comme on est au-delà de la valeur de pK_a+1 elle représente même une valeur supérieure à 90%du total de la concentration C₀.

Alors, on évoque ce que l'on appelle "l'effet de dilution", ou "l'approximation des acides forts" et l'on voit qu'à très faible concentration (ici le cas limite) un acide faible est complètement ionisé, comme s'il avait été un acide fort.

Si l'on pose la question du pH d'une solution d'acide éthanoïque de concentration C₀ égale à 10^-7mol.L^-1 alors on résoudra la question comme celle de l'acide chlorhydrique (acide fort) à la même concentration (voir plus haut dans mon cours). On tiendra donc compte des ions hydronium et hydroxyde de l'eau et l'on résoudra une équation du second degré en h.

En principe vous ne devez pas rencontrer de difficultés.

Je signale encore que cette question est du genre "académique" et qu'elle n'a, dans la pratique, aucun intérêt réel.

 Retour au plan du cours sur les pH des solutions aqueuses.
 
 

II.3.d. Cas d'une monobase faible.

 Retour au plan du cours sur les pH des solutions aqueuses.

On prendra le cas  du gaz ammoniac NH₃, mis en solution aqueuse, et dont la solution prend le nom d'"ammoniaque".

On cherchera à calculer le pHd'une solution d'ammoniaque de concentration C₀mol.L^-1.

L'équation chimique qui a lieu au sein de la solution  est la suivante:
                                              NH₃  +H₂O   NH₄⁺  +  HO^-.
Le pK_a du couple acidobasque NH₄⁺ / NH₃ est de 9.25 à 25 °C.
Ici, on voit apparaître  un équilibre qui sera plus facilement décrit par la constante d'équilibre K_b. En effet dans les produits de la réaction, à droite de l'équilibre, on trouve l'anion hydroxyde HO^-.
On aura donc K_bqui sera égal à: 
On écrira l'équation de conservation de la masse:

K_b  = 

Bien entendu on a K_a.K_b qui est égal à K_e.
A partir de là on résout une équation du second degré en  w, bref,  un trinôme en  w.
On arrive donc à l'équation suivante:

Cette méthode marche tout le temps.

On peut éventuellement préférer une version qui ne fait intervenir que la constante K_a et h.
Je donne cette seconde version pour ceux qui la préfèreraient.
On a K_a qui vaut:
On écrit de nouveau l'équation de conservation de la masse:

Donc, très simplement, on peut écrire que   (NH₄⁺)  = .

On conclut en éliminant la solution physiquement inacceptable et l'on arrive aisément au pH de la solution.

Bien entendu on doit retrouver, pour C₀ donné, le même résultat par la méthode en w et par la méthode en h. Sinon c'est qu'il y a une erreur quelque part.

A vous de choisir dorénavant la méthode qui vous paraît la plus aisée.

On peut également pour trouver le pH d'une monobase faible en solution aqueuse essayer des formules approchées. On va essayer de les retrouver.
Il faut tout d'abord tracer le diagramme de prédominance des espèces dissoutes pour, par exemple, le couple NH₄⁺/ NH₃ , dont le pK_avaut 9.25 à 25°C.

Comme pour le cas de l'acide éthanoïque, on retrouvera icia, qui sera appelé "degré de protonation" , relatif à l'évolution en fonction du pH de la forme protonée NH₄⁺ et 100-a, relatif à l'évolution en fonction du pH de la forme non protonée NH₃.
On reprend K_a.
                                      K_a  est égal à:
On écrit l'équation de conservation de la masse:

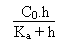                                       (NH₄⁺)  = et (NH₃) = 

                               (NH₄⁺)  = et : (NH₃) = 

Puisque  le "degré de protonation" aest égal à: , on arrive aux deux expressions suivantes, respectivement pour l'évolution de  NH₄⁺ et celle de NH₃.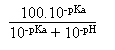

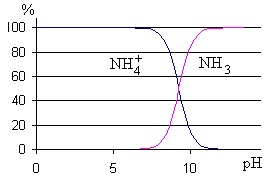
On voit sur le diagramme de prédominance que dans l'intervalle [pK_a-1;pK_a+1] les deux formes coexistent dans des proportions non négligeables l'une par rapport à l'autre.
Si le pH est inférieur à pK_a-1 alors c'est la forme protonée NH₄⁺ qui est majoritaire à plus de 90%.
Si par contre le pH du milieu est supérieur à pK_a+1 alors c'est la forme non protonée NH₃ qui est majoritaire à plus de 90%.
C'est cette dernière zone qui va permettre l'emploi éventuel des formules approchées.
En écrivant l'équation de conservation de la matière on aura alors:

Quand on reprend la constante d'équilibre K_b  =  on aura K_b qui se simplifiera  en : 

A partir de là on peut  remarquer que K_e  = w.h d'où w=  et comme  K_a.K_b = K_e

Cette formule n'est vraie, applicable si vous préférez, que si  le pH  cherché est strictement supérieur àpK_a + 1.
A défaut, il faut calculer le pH à l'aide de l'équation du second degré, comme précédemment.

A titre d'exercice on calculera, par la formule approchée, le pH d'une solution aqueuse d'ammoniaque de concentration C₀ égale à 0.1 mol.L^-1.
On comparera le résultat à celui trouvé avec l'équation du second degré.

On calculera également le pH d'une même solution, mais à 10^-5mol.L^-1 cette fois. Conclusion.

Enfin, on terminera avec le cas, encore une fois "académique" du calcul du pH d'une solution de monobase faible de concentration inférieure à 10^-6 mol.L^-1.

Prenons le cas du calcul du pH d'une solution d'ammoniaque de concentration égale à 10^-8 mol.L^-1.
Si la base avait été forte on aurait eu  un pH  compris entre 7 et 8: avec une monobase forte comme l'hydroxyde de sodium on avait trouvé, pour cette même concentration de 10^-8 mol.L^-1, un pH de 7.02.
Ici, comme la monobase est "faible" on ne peut avoir qu'un pH à la limite plus petit que 7.02.
On remarque, à l'aide du diagramme de prédominance des espèces dissoutes du couple NH₄⁺/NH₃, que c'est la forme protonée NH₄⁺ qui est largement majoritaire dans cet intervalle de pH.
On en conclut qu'à très faible concentration C₀, l'ammoniaque se comporte comme une monobase forte. On se ramène dès lors aux calculs précédents.
Pour une concentration en ammoniaque égale à 10^-8 mol.L^-1 on trouve un pH de 7.02.

 Retour au plan du cours sur les pH des solutions aqueuses.

II.3.e. Cas des polyacides.

  Cliquez ici pour le paragraphe sur les polyacides.

 Retour au plan du cours sur les pH des solutions aqueuses.