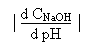
V.1. Mise en évidence expérimentale de l'effet tampon.
Retour au plan du cours sur les pH des solutions aqueuses.
Lorsqu'on dose 100 mL d' acide éthanoïque
de concentration C0 égale à 0.1 mol.L-1
par la soude de concentration Cb égale à 0.5 mol.L-1
on s'aperçoit autour de la demi-équivalence, vers V = 10
mL, qu'il y a une zone, pratiquement plate, dont les valeurs de pH
sont proches du pKa de l'acide éthanoïque (4.75 à 25°C),
et qui est fortement insensible, au niveau du pH, à l'ajout
de soude.
C'est le type même de l'effet tampon: un mileu
sera dit "tamponné" si, malgré l'ajout de soude, malgré
celui d'acide, malgré celui d'eau, son pH reste pratiquement constant.
On aura alors une solution "tampon".
Ce phénomène est très répandu
dans la nature: beaucoup de réactions biologiques se font à
un pH déterminé.
L' homme est lui même un mileu "tampon". En effet,
lorsqu'on boit, par exemple, un verre de vin le pH du vin est de
l'ordre de 3.50 à 4.00. Le pH sanguin est de l'ordre de 7.40. Lorsqu'on
boit un verre de vin le système biologique humain, du fait qu'il
est "tamponné", ne se trouve pas notoirement modifié
au niveau de son pH à cause de cela. Bien entendu si l'on boit trop
de vin on imagine les autres conséquences qui se font jour....Tout
est question de dose on s'en serait douté...(rires!!!). Mais les
problèmes sont alors dus à l'éthanol et pas au pH...
Retour au plan du cours sur les pH des solutions aqueuses.
V.2. Définition et mesure du pouvoir tampon b d'une solution.
Retour au plan du cours sur les pH des solutions aqueuses.
On définira une mesure de l'efficacité du pouvoir tampon de la solution précédente, acide faible neutralisé par une base forte, par la relation suivante:
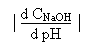
L'équation d'électroneutralité de la solution précédente, pour un volume V de soude versée est toujours égale à:
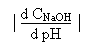 ,
c'est à dire
,
c'est à dire  .
. 
 = (H3O+).Ln10
= h.Ln10
= (H3O+).Ln10
= h.Ln10A partir de là on a aussi:
 =
= 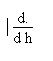
 =
=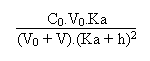
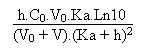 =
b
=
b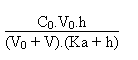
On en tire facilement la relation suivante:

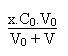
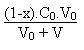
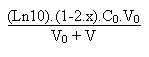
Remarque: ce raisonnement a été intégralement conduit dans le cas d'une base forte qui venait neutraliser en partie un acide faible. Si l'on avait eu le cas d'un acide fort qui venait neutraliser une base faible, par exemple le cas de l'acide chlorhydrique H3O+ + Cl- et de l'ammoniaque, le calcul aurait été mené de façon similaire. A ce moment là on aurait défini le pouvoir tampon b de la solution par la relation:
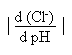
Retour au plan du cours sur les pH des solutions aqueuses.
V.3. Réalisation de solutions tampons.
Retour au plan du cours sur les pH des solutions aqueuses.
Il y a plusieurs méthodes.
Imaginons que nous voulions réaliser une solution
tampon de pH égal à 4.75, la valeur du pKa à 25°C
du couple CH3CO2H / CH3CO2-
Première méthode:
La façon la plus simple est sans doute de confectionner
une solution d'acide éthanoïque de concentration C0 égale
à 0.1 mol.L-1. Le volume V0 sera pris égal
à 250 mL.
On peut, à partir de là, calculer la masse
de cristaux de soude qu'on peut rajouter à la solution de façon
à la neutraliser de moitié.
Le nombre de moles d'acide éthanoïque étant
égal à C0.V0 soit numériquement
0.025 mol, il faudra apporter au milieu n NaOH = 0.0125 mol
de soude en cristaux pour effectuer la demi-neutralisation de la solution
suivant la réaction quantitative suivante:
Le pouvoir tampon b de la solution préparée sera égal à, vu que l'ajout de 0.5 g de soude s'est produit sans modification notable du volume de la solution:
Deuxième méthode:
On peut également chercher à neutraliser
à moitié les 250 mL de la solution d'acide éthanoïque
précédente par une solution aqueuse de soude. On aura tout
intérêt à utiliser une solution assez concentrée
de soude, de façon à limiter le facteur de dilution. On n'est
malgré tout pas obligé de travailler avec une solution concentrée.
Le choix se portera ici sur l'ajout d'une solution de
soude de concentration égale à 0.5 mol.L-1.
La demi équivalence sera atteinte pour un volume
de soude versée de 25 mL.
Le pouvoir tampon de la solution sera légèrement
inférieur à celui trouvé précédemment
mais on aura un volume plus grand de solution.
A ce niveau, comparable au niveau des pouvoirs tampons, le choix de la méthode vous appartient.
Troisième méthode:
On peut également mélanger des quantités égales d'acide éthanoïque en solution aqueuse et de base conjuguée, l'éthanoate de sodium.
Imaginons que l'on dispose de 250 mL de solution aqueuse
d'acide éthanoïque de concentration C0 égale
à 0.1 mol.L-1.
Le nombre de moles d'acide éthanoïque présent
dans cette solution est égal à 0.025 mol.
Il faudra dans ce cas ajouter à la solution
aqueuse 0.025 mol d'éthanoate de sodium.
L'éthanoate de sodium NaOAc, CH3CO2Na,
a pour formule cristallisée (CH3CO2Na, 3H2O).
La masse molaire des cristaux devra tenir compte du fait
que trois molécules d'eau cristallisent avec un groupement formulaire.
La masse molaire M de l'éthanoate de sodium
sera alors égale à : 124 g.mol-1.
Il faudra donc peser une masse m de cristaux égale
à 3.10 g et rajouter ces 3.10 g dans la solution aqueuse de façon
à obtenir une solution tampon de pH égal à 4.75 à
25°C.
Si l'on admet que la dissolution des cristaux d'éthanoate
de sodium s'est faite sans augmentation de volume de la solution on aura
confectionné une solution tampon de pouvoir tampon
b égal à:
0,2.0,5.0,5.Ln10, soit 0.115 mol.L-1.
En effet la concentration totale en acide éthanoïque
et éthanoate de sodium devient égale à 0.1 + 0.1 =
0.2 mol.L-1, et les espèces moléculaire CH3CO2H
et ionisée CH3CO2- sont présentes
dans les proportions moitié-moitié.
Question d'ordre pratique:
Comment réaliser un tampon pH 7, bref le tampon servant à étalonner les pH-mètres?
On utilisera le pKa2 de l'acide phosphorique,
de valeur numérique égale à 7.20 à 25°C
et correspondant au couple dihydrogénophosphate / hydrogénophosphate,
soit H2PO4- / HPO42-.
On préparera par exemple 250 mL de solution tampon.
On préparera la solution à l'aide de cristaux
de chacun des hydrogénosels.
La formule du dihydrogénophosphate de sodium cristallisé
est: (NaH2PO4, H2O). La masse molaire
est de 137.99 g.mol-1.
Cela ne veut pas dire que l'hydrogénosel est "mouillé"
quand on le touche, mais tout simplement que le groupement formulaire cristallise
en emprisonnant une molécule d'eau par groupement. Bref il y a ici
une mole d'eau qui accompagne forcément une mole de dihydrogénophosphate
de sodium. Il faut tenir compte de cela lors de la pesée.
La formule de l'hydrogénophosphate de disodium
cristallisé est: (Na2HPO4, 2H2O).
Sa masse molaire est de 177.99 g.mol-1.
La formule donnant le pH de la solution en fonction des concentrations des espèces acido-basiques est la suivante:

Bilan:
Dans une fiole de 250 mL on ajoutera une masse
m NaH2PO4,H2O égale
à 0,00395.137,99 soit 0.545 g.
On ajoutera une masse m Na2HPO4,2H2O
égale à 0,0025.177,99 soit 0.445 g.
On dissoudra les cristaux et l'on ajoutera de l'eau qsp
250 mL.
La solution tampon est prête.
Son pouvoir tampon b est
égal à:
Remarque: pour être encore plus rigoureux il faudrait,
non pas considérer les concentrations des ions mais leurs "activités".
Pour des faibles concentrations il y a une concordance assez
bonne entre ces deux notions. Pour des calculs de "première année"
on en restera là. En Licence de Chimie on effectuera les corrections
à cette approximation...
Lorsque les concentrations dépassent les 0.2 mol.L-1
il vaut mieux appliquer les termes correctifs donnés par la
méthode de DEBYE-HUCKEL qui tient compte de la force ionique I
de la solution.
Retour au plan du cours sur les pH des solutions aqueuses.
Suite du cours de chimie sur les pH des solutions aqueuses. Cliquer ici.