2Na+ + CO32- + H3O+ + Cl-
Retour au plan du cours sur les pH des solutions aqueuses.
On se proposera d'étudier la courbe de dosage d'un
mélange d'une base forte, la soude, avec une polybase faible, le
carbonate de sodium.
Cet exercice, loin d'être académique, est
un problème qui se pose fréquemment en TP (voir d'ailleurs
le TP sur le sujet) lorsqu'on utilise une solution aqueuse d'hydroxyde
de sodium qui est trop ancienne. La soude pompe en effet le dioxyde de
carbone de l'air et le transforme en carbonate de sodium. Ainsi il est
toujours très recommandé de ne pas effectuer le moindre dosage
avec la soude sans avoir au préalable étalonné de
nouveau le flacon. La concentration recalculée en ions hydroxyde
permettra alors de faire un dosage dans les meilleures conditions. L'idéal
est de toujours opérer malgré tout avec un flacon de soude
très fraîchement préparée.
On étudiera ici la courbe de dosage d'une solution aqueuse de volume initial V0 égal à 100 mL, contenant de l'hydroxyde de sodium NaOH à la concentration C1 de 0.1 mol.L-1 et du carbonate de sodium à la concentration C2 de 0.050 mol.L-1. Le dosage sera effectué par une solution aqueuse d'acide chlorhydrique de concentration Ca égale à 0.5 mol.L-1.
On rappellera que les deux couples acido-basiques du dioxyde
de carbone, qui interviennent ici, sont respectivement:
CO2, H2O / HCO3-
pKa1 = 6.40; HCO3-/CO32-
pKa2 = 10.30.
Lorsqu'on fait l'expérience du dosage on voit
sur la courbe deux sauts de potentiel.
Le premier saut correspond au dosage intégral
de la soude et à la neutralisation de la première fonction
basique du carbonate de sodium. On se retrouva alors dans le milieu réactionnel
en présence d'une solution aqueuse de chlorure de sodium et d' hydrogénocarbonate
de sodium.
Le second saut correspond au dosage intégral de
l'hydrogénocarbonate de sodium et à sa trasformation en chlorure
de sodium et dioxyde de carbone en solution aqueuse.
Les équations du dosage seront alors:
Première partie de la courbe: avant le premier
saut de potentiel.
Deuxième partie après le premier saut de potentiel:
Au-delà de la deuxième partie, du second saut de potentiel, on se retrouve avec un excès d'acide chlorhydrique. Ce sera lui qui imposera le pH de la solution.
On cherchera à calculer les volumes équivalents
V1 et V2, correspondant respectivement aux deux sauts
de potentiel précédents.
Pour neutraliser un volume V0 de
soude à la concentration de 0.1 mol.L-1 il faut un volume
V d'acide chlorhydrique à 0.5 mol.L-1 égal à
20 mL.
Pour neutraliser un volume V0 de carbonate
de sodium à la concentration de 0.05 moL.L-1 par de l'acide
chlorhydrique à 0.5 mol.L-1 il faut un volume V égal
à 10 mL de cet acide.
En conséquence le volume V1 sera égal
à 20 + 10 soit 30 mL.
Pour neutraliser le reste, c'est à dire l'hydrogénocarbonate
de sodium formé lors de la première partie, on devine qu'il
faut ajouter un volume d'acide chlorhydrique égal à 10 mL
pour arriver au résultat. Les coefficients stoechiométriques
sont en effet constamment égaux à 1.
Le volume V2 sera donc égal, si on
compte depuis l'origine, à la valeur 30 + 10, soit 40 mL.
On cherchera à calculer les valeurs des pH pour
tous les points de la courbe. On la découpera en trois parties:
Première partie ente V = 0 et V = V1,
soit 30 mL.
Deuxième partie: entre V = 30 et V = 40 mL.
Troisième partie: au-delà de 40 mL.
Première partie:
On calculera tout d'abord les pH pour les deux valeurs
extrêmes.
Lorsque V = 0 mL le pH du milieu est imposé par
la soude, base forte. Le pH sera donc égal à:
Entre ces deux valeurs il faudra résoudre l'équation
de l'électroneutralité de la solution pour arriver au pH
de la solution.
On aura alors:
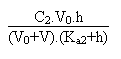
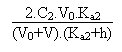
Deuxième partie: entre V = 30 et V = 40 mL.
On part d'un pH de 8.35 à V = 30 mL.
Lorsque V = 40 mL on est en présence d'une solution
aqueuse de dioxyde de carbone, de concentration C égale à:
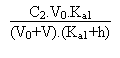
Si l'on postule que le pH sera acide il faudra alors résoudre l'équation du second degré suivante:
Troisième et dernière partie: au-delà de V = 40 mL.
La concentration des ions hydronium provenant de l'acide chlorhydrique et qui imposeront le pH de la solution sera égale à:
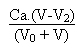
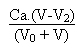
Si le volume V d'acide tend vers l'infini on tend vers un ph égal à 0.3.
Retour au plan du cours sur les pH des solutions aqueuses.
IV.8. Dosage d'un mélange d'acide chlorhydrique et d'acide phosphorique.
Retour au plan du cours sur les pH des solutions aqueuses.
On se propse d'étudier le dosage de 100 mL d'une
solution aqueuse contenant de l'acide chlorhydrique à la concentration
C1 égale à 0.1 mol.L-1 et de l'acide
phosphorique à la concentration C2 égale à
0.05 mol.L-1 par une solution aqueuse d' hydroxyde de sodium
à 0.5 mol.L-1.
On rappellera les valeurs des trois pKa de l'acide phosphorique:
2.15; 7.20 et 12.10 à 25°C.
Lorsqu'on fait l'expérience on constate l'existence
de deux sauts de potentiel sur la courbe.
Le premier saut intervient lorsqu'on a fini de consommer
tous les ions hydronium provenant de l'acide chlorhydrique et lorsqu'on
a fini de doser la première acidité de l'acide phosphorique.
Les réactions qui interviennent sont les suivantes.
On donnera pour chacune d'elles la valeur de la constante de réaction
Kr qui leur est associée.
Ces deux valeurs sont très supérieures à l'unité. si l'aspect cinétique des réactions va dans le même sens que l'aspect thermodynamique, alors ces deux réactions sont très favorisées dans le sens gauche vers droite et elles deviennent quantitatives. C'est ce que dans la pratique on constate en effet.
Le second saut de potentiel intervient lorsqu'on a fini
de doser la seconde acidité de l'acide phosphorique.
L'équation du dosage est alors la suivante:
On calculera les volumes V1 et V2
qui correspondent aux deux sauts de potentiel.
On constate qu'il faut 20 mL de soude à la concentration
Cb égale à 0.5 mol.L-1 pour neutraliser
les 100 mL d'acide chlorhydrique de concentration C1 égale
à 0.1 mol.L-1.
Il faut alors 10 mL de soude en supplément pour
neutraliser la totalité de la première acidité de
l'acide phosphorique présent à la concentration C2
égale à 0.05 mol.L-1.
Le volume V1 sera donc égal à
20 + 10 soit 30 mL.
Du fait que tous les coefficients stoechiométriques
des réactions sont égaux à 1 il faudra alors 10 mL
de soude supplémentaires pour neutraliser la totalité de
la seconde acidité de l'acide phosphorique.
Le volume V2, si l'on compte les volumes à
partir de l'origine sera donc égal à 30 + 10 soit 40 mL.
On découpera la courbe de dosage en trois parties.
Première partie: de V = 0 à V = 30 mL de
soude versée.
Deuxième partie: de V = 30 à V = 40 mL
de soude versée.
Troisième et dernière partie: au-delà
de V = 40 mL.
Première partie: de V = 0 à V = 30 mL.
On calculera les valeurs des deux pH extrêmes.
Lorsque V = 0 mL de soude versée le pH du milieu
est celui qu'impose l'acide chlorhydrique.
Le pH initial aura pour valeur:
Entre ces deux valeurs extrêmes le pH, qui sera toujours et "forcément" acide, sera donné par la résolution de l'équation de l'électroneutralité de la solution suivante:
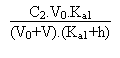
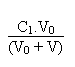
On arrivera alors, en réarrangeant tous les termes, et sans se tromper (!!!) à l'équation du second degré suivante:
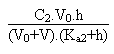
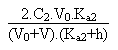
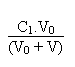
Si au contraire on postule que le pH sera basique on aura à résoudre l'équation d'électroneutralité suivante:
Troisième et dernière partie: au-delà
de V = 40 mL.
A ce moment là ce sera la soude qui imposera le
pH de la solution.
La concentration des ions hydroxyde sera alors égale
à:
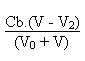
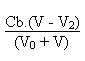
Suite du cours sur les pH des solutions aqueuses. cliquer ici.