IV. Les courbes de dosage acidobasiques.

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.1.Cas du dosage d'un acide fort par une base forte.

 Retour au plan du cours sur les pH des solutions aqueuses.

On prendra l'exemple du dosage d'une solution d'acide chlorhydrique H3O+ + Cl- de concentration C0 égale à 0.1mol.L-1, de volume V0 égal à 100 mL, par la soude Na+ + HO- de concentration Cb égale à 0.5 mol.L-1.
L'équation du dosage est:

Na+  + HO-  +  H3O+  +  Cl- Na+  +  Cl-  +  2H2O
La constante de réaction Kr est égale à 10+14.
Du point de vue thermodynamique, si l'aspect cinétique le permet, la réaction est quantitative, fortement déplacée vers la droite.

La courbe de dosage peut se découper en trois parties distinctes, qui ne  présenteront aucune discontinuité.

Première partie: avant l'équivalence.
Deuxième partie: à l'équivalence.
Troisième et dernière partie: après l'équivalence.

Première partie.
Afin de calculer chaque point de la courbe de dosage avant l'équivalence il faut faire un bilan de matière initial sur la solution d'acide chlorhydrique.
Le nombre de moles d'ions hydronium contenu initialement dans la solution est égal à: C0.V0.
Numériquement cela fait n  H3O+ =  0,1.0,1 soit 0.01 mol.
Si l'on ajoute un volume V de soude dans la solution d'acide chlorhydrique le nombre de moles d'ions hydroxyde apporté est égal à Cb.V.
Etant donné la réaction entre les ions hydronium et les ions hydroxyde pour donner de l'eau; étant donné que V est inférieur à Ve le volume équivalent, on aura un nombre de moles d'ions hydronium qui restera en solution qui sera égal à: C0.V0 - CbV
Le volume de la solution étant devenu égal à V0  +  V, la concentration des ions hydronium restant en solution après ajout d'un volume V de soude sera égale à:

(H3O+) = 
Le pH sera donné en prenant le cologarithme de l'expression suivante.
Dans l'exemple choisi le pH sera égal à:

pH = log(100 + V) - log(10 - 0,5.V)

On pourra s'amuser à calculer le pH de la solution en fonction de V, avant l'équivalence, en faisant par exemple varier V d'un millilitre à chaque fois.

C'est la méthode "traditionnelle".

A l'heure d'Internet il est beaucoup plus intéressant de programmer une telle équation avec Excel. On obtient un listing de valeurs numériques et la courbe.

Deuxième partie de la courbe: l'équivalence.
On se ramène alors au calcul du pH d'une solution d'acide fort exactement neutralisée par une base forte. On a démontré au chapitre précédent que le pH à l'équivalence valait alors 7 à 25°C.
Ici le volume équivalent vaut 20 mL. le pH aura alors pour valeur 7.

Troisième partie de la courbe: après l'équivalence.
On aura versé depuis le départ un volume supérieur à 20 mL pour accéder à cette portion de courbe.
Si l'on appelle V ce volume total de soude versée (par exemple 25 mL) le nombre total de moles d'ions hydroxyde apportés est égal à Cb.V.
Comme 1 ion hydroxyde réagit avec 1 ion hydronium de façon quantitative pour donner de l'eau, la quantité d'ions hydroxyde en excès sera égale à: Cb.V - C0.V0.

La concentration des ions hydroxyde lorsqu'on aura versé V mL de soude dans la solution d'acide chlorhydrique sera alors égale à:

(HO-) = 
Le pH de la solution sera donné en écrivant:
pH = 14 + log(HO-)

Dans l'exemple qui est choisi il faudra écrire que :

pH = 14 + log (0.5.V -10) - log(100 + V)

L'ensemble de ces résultats sera listé sur papier et une courbe publiée.

A titre d'exercice on peut s'amuser à calculer le pH en fonction de V pour une solution aqueuse d'acide bromhydrique, de formule H3O+ + Br- , de volume V0 égal à 50 mL, de concentration C0 égale à  0.02 mol.L-1, par l'hydroxyde de potassium K++ HO- de concentration Cb égale à  0.03 mol.L-1.

On s'amusera alors aussi à calculer,  en fonction du volume d'agent titrant versé,  le pH d'une solution de soude de concentration Cb égale à 0.1 mol.L-1 , de volume V égal à 100 mL, par une solution aqueuse d'acide iodhydrique de formule H3O++ I- de concentration égale à 0.2 mol.L-1.

Il existe bien sûr une "autre" méthode de calcul de chaque point de la courbe, que l'on soit avant, pendant ou après l'équivalence.
Cette méthode repose sur la résolution de l'équation d'électroneutralité.

h  +  (Na+)  = w  + (Cl-)
La concentration des ions sodium est égale à:
(Na+) = 
La concentration des ions chlorure est égale à:
(Cl-) = 
Comme on a Ke = h.w  il est alors facile d'exprimer w en fonction de h et l'on tombe sur une équation du second degré en h qui permet d'accéder au pH très facilementet ce, quel que soit le volume V de soude versé.
Chacun choisira "sa" méthode.

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.2.Cas du dosage d'un acide faible par une base forte.

 Retour au plan du cours sur les pH des solutions aqueuses.

On cherchera à calculer le pH d'une solution aqueuse d'acide éthanoïque CH3CO2H, de concentration C0 égale à 0.1 mol.L-1, de volume V0  égal à 100 mL, par une solution aqueuse d'hydroxyde de sodium Na+ + HO-, de concentration Cb égale à 0.5 mol.L-1.
On rappelle que le pKa du couple CH3CO2H/CH3CO2- est égal à 4.75 à 25°C et que la constante d'autoprotolyse de l'eau Ke  a pour valeur 10-14 toujours à 25°C.

L'équation du dosage est:

CH3CO2H  +  Na+  +  HO-  CH3CO2-  +  Na+  + H2O
La constante de réaction Kr est égale au rapport de la constante d'acidité Ka de l'acide éthanoïque par la constante d'autoprotolyse de l'eau Ke. Kr vaut donc 1.78.109. La réaction est quantitative, du point de vue thermodynamique,  de la gauche vers la droite si la cinétique le permet.

Le calcul des points de la courbe pourra se faire de plusieurs façons.
La façon la plus "traditionnelle" est d'écrire l'électroneutralité de la solution et de faire des hypothèses raisonnables sur le pH de la solution, et ce, que l'on soit avant, pendant ou après l'équivalence.
On écrira alors:

h  +  (Na+)  =  w  +  (AcO-)
La concentration de l'ion sodium, ion spectateur, sans aucune influence sur la valeur du pH, sera égale à:
(Na+)  = 
La concentration de l'anion éthanoate AcO- sera égale à:
(AcO-) = 
On a tenu compte de la concentration corrigée de l'acide éthanoïque global, en raison du facteur de dilution, et de l'expression désormais "habituelle" de la forme basique du couple acide/base en fonction de Ka et de h.On l'a démontrée lors de l'établissement du pH d'un monoacide faible et du sel d'un acide faible et de base forte.

Afin d'éviter la résolution d'une équation de degré trois on fait alors des hypothèses raisonnables sur le pH attendu de la solution.
On postule par exemple qu'avant l'équivalence le pH sera acide.
A ce moment on raye de l'équation d'électroneutralité le terme w. On arrive après réarrangement des termes restants à une équation du second degré.
Cette équation du second degré en h aura ses termes qui seront fonction du volume V versé de soude. Pour chaque volume V versé on aura des termes différents et, par conséquent,  une équation du second degré différente à chaque fois.
L'équation s'écrit littéralement, sauf erreur de ma part (moi les maths vous savez c'est pas trop mon fort!!!):

(V0 + V).h2  + (Ka.V0  +  Ka.V  +  Cb.V).h  -C0.V0.Ka  +  Cb.V.Ka  =  0
Les concentrations C0 et Cb sont exprimées en mol.L-1 et les volumes V0 et V sont exprimés en mL. Je vous conseille en fait de remplacer au plus vite par leurs valeurs numériques toutes ces constantes et ces paramètres car sinon c'est très facile de se "planter"....
On résout alors l'équation pour chaque V.
Cette équation a été établie pour un pH censé être acide.
Et si le pH trouvé grâce à cette formule  est basique?
Alors c'est que l'hypothèse de travail était fausse. Il ne fallait pas dans l'électroneutralité rayer w devanth  mais h  devant w.
On reprend alors l'électroneutralité, on revient au fait que Ke est égal à h.w et on arrive à l'équation du second degré suivante:
Cb.V.h2  +  (Cb.V.Ka  -  C0.V0.Ka  -  Ke.V).h  -  Ka.Ke.V0  =  0
Ici aussi je vous conseille de remplacer par leurs valeurs numériques toutes ces constantes et ces paramètres au plus tôt. L'équation apparaît alors vraiment simple alors que sous forme littérale elle est vraiment monstrueuse. Enfin moi je trouve....

A ce moment là la résolution conduit au pH cherché...
On peut dès lors tracer la courbe avec un listing de points.

Je vous donne l'exemple du calcul du pH de la solution pour la demi-équivalence, histoire de tester la formule que j'ai établie.

Le volume V correspondant à la demi-équivalence est V = 10 mL.
La concentration de la soude vaut 0.5 mol.L-1, celle initiale de l'acide 0.1 mol.L-1. La constante d'acidité de l'acide éthanoïque vaut 1.78.10-5.
En remplaçant par leurs valeurs numériques chacun des termes de l'équation du second degré pour un pH censé être acide on arrive à devoir résoudre:

110.h2  + 5.002.h  -  8.9.10-5  =  0
On résout et on arrive à un pH de... 4.75, bref à pH égal à pKa, ce qui est très fréquent à la demi équivalence.

Yo!!!!

A vous de continuer en prenant par exemple V égal à 7.5 mL ou V égal à 13 mL, histoire de calculer un petit peu...
 

Aujourd'hui il y a une autre méthode.
On travaille avec Excel et on fait résoudre à la machine l'équation d'électroneutralité complète, incluant donc h et w, puis on sélectionne les valeurs physiquement acceptables.
L'équation complète qu'on va fournir à Excel est la suivante:

(V+V0).h3  + [Cb.V + Ka.(V+V0)].h2 + [Cb.V.Ka -Ke.(V+V0) -C0.V0.Ka].h  -Ka.Ke.(V+V0) = 0
Je précise que les valeurs de V et de V0 sont données en mL. Les concentrations C0 et Cb sont données en mol.L-1. On s'est bien sûr arrangé pour qu'il n'y ait pas de problèmes de conversion d'unités. En effet, on a à chaque fois des rapports de nombres ayant les mêmes unités et on retombe ainsi facilement sur ses pattes.
Avec les valeurs de l'exemple précédent on arrive à une équation qui s'écrira, en fonction de V, en tenant compte des ordres de grandeur respectifs de chacun des termes les uns vis à vis des autres:

(100 + V).h3 + [0.5.V + 1.78.10-3].h2 + (8.9.10-6.V - 1.78.10-4).h -1.78.10-19.(100 + V) = 0

A ce moment là, sachant que les solutions physiquement acceptables sont comprises entre 10-14 et 1, bref pour des pH compris entre 0 et 14, le logiciel calcule chaque valeur de pH après avoir calculé chacun des termes du polynôme et résolu l'équation du troisième degré.
C'est bien à cela que servent les machines, à faire des travaux très pénibles...

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.3.Cas du dosage d'une base faible par un acide fort.

 Retour au cours sur les pH des solutions aqueuses.

On cherchera à calculer les valeurs des pH de la courbe de neutralisation d'une monobase faible, l'ammoniac NH3, de concentration Cb égale à 0.1 mol.L-1, de volume Vb égal à  100 mL , par l'acide chlorhydrique H3O+ + Cl-, de concentration Ca égale à 0.5 mol.L-1.On versera à chaque fois un volume V d'acide chlorhydrique dans la solution ammoniacale.

L'équation de l'électroneutralité est la suivante:

h  +  (NH4+)  =  w  +  (Cl-)
L'anion chlorure Cl- est spectateur, il n'influera pas sur la valeur du pH de la solution. Sa concentration sera égale à:
(Cl-) = 
La concentration du cation ammonium s'écrira, tenant compte de facteur de dilution lors de l'ajout d'acide, en fonction de Ka et de h, comme de "coutume" (voir parties sur le pH d'une monobase faible et sur le pH d'un sel d'acide fort et de base faible):
(NH4+) = 
A partir de là deux possibilités: soit la méthode "traditionnelle" soit la méthode complète avec Excel.

Commençons par la méthode traditionnelle.

On fait des hypothèses raisonnables sur la valeur attendue du pH et on raye dans l'équation de l'électroneutralité soit h devant w, soit w devant h.
Si jamais en rayant, par exemple,  h devant w on résout l'équation de l'électroneutralité et qu'on aboutit à un pH acide alors il faut reprendre l'équation de l'électroneutralité, rayer w devant h et puis résoudre. la méthode artisanale est faite de tâtonnements, d'erreurs mais on arrive toujours à retomber sur ses pieds.

Si l'on postule que le pH est basique on a à résoudre l'équation suivante, sachant que Ke est égal à h.w:

(Cb.Vb -Ca.V).h2  -[(V + Vb).Ke +Ca.Ka.V].h -Ka.Ke.(V+Vb)  =  0

Je vous conseille vivement de très vite remplacer les expressions littérales par des valeurs numériques. L'équation du second degré vous paraîtra alors pour ce qu'elle est, à savoir une équation toute bête.

Si jamais le pH n'est pas basique mais au contraire acide, alors il faut reprendre l'équation d'électroneutralité, rayer w devant h et on arrive alors à une équation du second degré qui a l'allure suivante:

(V + Vb).h2  + [Ka.(Vb+V) + Cb.Vb -Ca.V].h  -Ca.Ka.V  =  0
Même remarque que précédemment quant à la vive recommandation de très vite passer aux valeurs numériques afin de démystifier cette équation du second degré qui est "toute bête"...On arrive facilement alors aux résultats et l'on peut tracer la courbe donnant le pH en fonction de V.

Je donne l'exemple du calcul du pH de la solution lorsque le volume d'acide chlorhydrique versé est égal à 10 mL, bref lorsqu'on est à la demi-équivalence, donc un pH attendu de 9.25:
Vu que Ca = 0.5 mol.L-1, que Cb = 0.1 mol.L-1, que Vb = 100 mL et que V = 10 mL, en remplaçant dans l'équation censée donner un pH basique on arrive à l'équation du second degré suivante:

5h2  -2.81.10-9.h  -6.18.10-22  = 0
La résolution conduit à pH = 9.25, bref, à pKa.Ce qui est assez fréquent à la demi équivalence. La formule a donc l'air correcte...
 
 

Si au contraire on prend la méthode complète avec Excel on arrive à l'équation de degré trois suivante:

(V+Vb).h3 + [Ca.V -Cb.Vb - Ka.(V + Vb)].h2  + [Ca.Ka.V + Ke.(V +Vb)].h + Ka.Ke.(V + Vb) = 0

On exprimera V et Vb en mL , Ca et Cb en mol.L-1.
L'équation s'écrira dans l'exemple qui est choisi, en tenant compte des ordres de grandeur respectifs des termes les uns vis à vis des autres:

(100+V).h3  +(0.5.V - 10).h2 + 2.81.10-9.V.h + 5.6.10-24.(100 +V)  = 0

Excel fournira un listing de valeurs et la courbe.

A vous de jouer maintenant.

 Retour au plan du cours sur les pH des solutions aqueuses.
 

IV.4. Calcul de la courbe de dosage d'un acide faible par une base faible.

Retour au plan du cours sur les pH des solutions aqueuses.

On cherchera à calculer les valeurs de pH des différents points de la courbe de neutralisation de l'acide éthanoïque, de concentration C0 égale à 0.1 mol.L-1, par l'ammoniaque de concentration égale à 0.5 mol.L-1. Le volume initial de la solution d'acide éthanoïque sera pris égal à 100 mL et l'on rappelle que les pKa respectifs de l'acide éthanoïque et de l'ion ammonium sont, dans l'eau, à 25°C, égaux à 4.75 et 9.25.

L'équation chimique du dosage est la suivante:

CH3CO2H  +  NH3CH3CO2- +  NH4+
La constante de réaction Kr est égale à 10-4.75+9.25 , soit 10+4.5, soit 3.17.104. Comme cette valeur est très supérieure à l'unité, si la cinétique de réaction le permet, alors la réaction est quantitative de la gauche vers la droite. C'est elle qui est la réaction prépondérante ici.
C'est elle qui imposera les diverses concentrations des espèces dissoutes puisque toutes les autres réactions possibles pour les espèces présentes ont des constantes très nettement inférieures à l'unité.

La résolution complète du problème passe par la résolution de l'équation de l'électroneutralité.
On aura alors:

h  +  (NH4+)  = w  +  (CH3CO2-)
La résolution est celle d'un polynôme de degré supérieur à deux. Il faut tenir compte des facteurs de dilution et des pKa respectifs de l'acide éthanoïque et de l'ion ammonium.
Il y a une méthode plus "simple" mais qui est aussi plus "limitée". Ca dépend de ce dont on a besoin et des conditions opératoires.
Cette méthode simple est celle où les concentrations en acide et en base sont "conséquentes", c'est à dire de l'ordre de 10-1 mol.L-1 par exemple.C'est le cas le plus fréquent pour les problèmes ordinaires qu'on peut poser à des étudiants.

J'en donne les grandes lignes ci-dessous.

A l'instant initial il faudra juste calculer le pH d'une solution d'un monoacide faible de concentration et de pKa connus.

Au cours du dosage, avant l'équivalence, on aura la possibilité d'utiliser la constante d'acidité Ka de l'acide éthanoïque, notamment sous sa forme logarithmique, afin de calculer le pH.
On aura alors:

pH  = pKa  +  log
Que valent, en fonction du volume V de base versée dans le volume V0 d'acide éthanoïque, les concentrations respectives en anion éthanoate et en acide éthanoïque sous sa  forme moléculaire?
Le nombre de moles initial d'acide éthanoïque, sous forme moléculaire et ionisée,  est égal à C0.V0.
Dans le cas le plus général, à savoir que l'acide est très faiblement dissocié au départ, on a:
(CH3CO2-) = 
Dès lors, vu l'existence de la réaction prépondérante, on aura:
(CH3CO2H) = 
A partir de là il est facile d'exprimer le pH en fonction de toutes les données expérimentales.
On arrive alors à:
pH  =  pKa  +  log
On vérifie qu'à la demi-équivalence on a bien comme valeur de pH la valeur pH = pKa du couple acide éthanoïque/ion éthanoate, soit 4.75 à 25°C.

Quand est-ce que cette formule est mise en défaut?

C'est lorsqu'on part d'une valeur de pH qui est supérieure au pKa du couple acide éthanoïque/ion éthanoate. C'est le cas lorsque la concentration en acide éthanoïque au départ est faible et que l'hydrolyse de la molécule d'acide conduit à une quantité non négligeable d'anion éthanoate dès le départ.
Cela se retrouve aussi lorsqu'au lieu de prendre l'acide éthanoïque on prend un acide plus fort et qu'on surajoute une autre "difficulté" , je veux parler d'une faible concentration en acide au départ.
A ce moment là le mieux à mon avis est de résoudre l'équation d'électroneutralité de la solution:

h + (NH4+) = w + (CH3CO2-)
On remplacera (NH4+) et (CH3CO2-) par leurs expressions en fonction des constantes d'acidité Ka de chaque couple acidobasique qui intervient (celui de l'acide éthanoïque et celui de l'ion ammonium), de h et des concentrations corrigées.
On pourra faire des approximations raisonnables sur la valeur attendue du pH et on résoudra l'équation correspondante, de degré sûrement supérieur à 2.
Je ne pense pas qu'il faille ici, à moins que vraiment je reçoive un nombreux  courrier  à ce sujet, rentrer dans les détails. Ce cas d'un dosage d'un acide faible à faible concentration par une base faible ne présentant, et je pèse mes mots, qu'un intérêt limité.
Enfin je reste à votre disposition s'il faut aller au charbon à ce sujet.

A l'équivalence on se retrouve avec le calcul du pH d'un sel de base faible et d'acide faible. On essaiera la formule magique:

pH = 0,5.(pKa1 + pKa2)
ou, à défaut,  on se reportera au paragraphe correspondant dans le cours on line, si jamais cette formule était prise en défaut.

Après l'équivalence on se retrouvera avec un mélange dans des proportions conséquentes d'ammoniac NH3 et d'ion ammonium. On calculera le pH de la solution en utilisant la formule:

pH = pKa + log
où pKa désigne le cologarithme de la constante d'acidité de l'ion ammonium, soit la valeur 9.25 à 25°C.
On aura alors:
(NH3) =
et, bien sûr,
(NH4+) = 
Bref, on aura comme expression :
pH = pKa + log 
Pour en finir avec cette méthode simple je ne saurais trop vous recommander de faire l'expérience au labo vous mêmes si jamais vous le pouvez. Les calculs c'est bien beau mais la pratique c'est MIEUX!!!!
Et si cette méthode "passe-partout" s'avérait donner des résultats erronés eh bien je vous conseillerais de résoudre l'équation d'électroneutralité complète avec l'aide du Solveur d'Excel.

Pour les "mordus" de ces dosages d'acide faible par une base faible je poserai comme question ultra "vache" le calcul des pH de la courbe de dosage de 100 mL d'une solution aqueuse d'acide oxalique (diacide faible), de concentration égale à 0.1 mol.L-1 par l'ammoniaque de concentration 0.5 mol.L-1.
Amusez-vous bien!!!!!!!
Pour vous aider je vous donne l'équation d'électroneutralité qu'il faudrait résoudre alors:

h  +  (NH4+)  = w + (HO2C-CO2-)  +  2.(-O2C-CO2-)
Cette équation de degré élevé a au moins le très grand mérite de marcher tout le temps.

Mais la chimie est elle un jeu mathématique? Ne se trompe t-on point de sphère?

Je vous souhaite bien du "plaisir" et vous encourage alors, plutôt que de perdre du temps, à faire la manip directement.C'est un excellent exercice expérimental, incontournable,  mais j'espère surtout que personne n'aura l'idée saugrenue de poser à des étudiants de première année une question aussi difficile. Il y a tant de choses intéressantes à découvrir de par la chimie autres que cet exercice de pH. Voyage à Chimiland....

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.5. Dosage d'un polyacide faible par une monobase forte.

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.5.a. Conditions sur les valeurs consécutives de deux pKa d'un polyacide faible pour doser séparément deux acidités.

 Retour au plan du cours sur les pH des solutions aqueuses.

Soit un diacide H2A. Il possède deux constantes d'acidité successives, caractérisées par leurs pKa respectifs, pKa1 et pKa2.
Si l'on dose cet acide par une base forte quelle est la condition que doivent remplir les deux pKa pour qu'on puisse avoir, par exemple, lors du dosage de la première acidité, 98% du total qui soit sous la forme HA-, avec seulement 1% de forme H2A et juste 1% de forme A2-?

Il faut écrire l'expression littérale de chacune des constantes Ka1 et Ka2, en fonction de h et des concentrations des espèces dissoutes H2A, HA- et A2-.Ces expressions restent vraies quel que soit le pH de la solution et, par conséquent, sa composition en espèces dissoutes.
On fait le rapport de Ka1 sur Ka2 et on arrive à:

  = 
En remplaçant (H2A), (HA-) et (A2-) par  leurs  valeurs numériques on arrive à:
= 
En prenant le logarithme de l'expression on arrive à:
DpKa = pKa2 - pKa1 = 3.98
valeur qu'on arrondira à 4.00.
Donc, si
DpKa = 4
alors on dira qu'on peut doser séparément les deux acidités consécutives d'un diacide ou d'un polyacide quelconque.

IV.5.b.a. Dosage d'un diacide faible,  l'acide sulfureux, ou dioxyde de soufre en solution aqueuse.Cas où la différence de pKa est supérieure à 4.

 Retour au plan du cours sur les pH des solutions aqueuses.

Le dioxyde de soufre en solution aqueuse SO2 aq , ou SO2,H2O,ou H2SO3,  est susceptible de donner deux équilibres acidobasiques, caractérisés par deux constantes d'acidité Ka1 et Ka2 respectivement.
Nous aurons donc:

SO2  +  2H2O H3O+  +  HSO3-
Equilibre caractérisé par la constante Ka1 et, par conséquent, par le pKa1 de valeur 2.0 à 25°C.
Nous aurons aussi:
HSO3-  +  H2O H3O+  +   SO32-
Equilibre caractérisé par la constante d'acidité Ka2, et par conséquent, par le pKa2 de valeur 7.6 à 25°C.

Nous chercherons à calculer les points de la courbe de dosage d'une solution aqueuse de dioxyde de soufre de concentration C0 égale à 0.1 mol.L-1 et de volume V0 égal à 100 mL, par une base forte, l'hydroxyde de sodium de concentration Cb égale à 0.5 mol.L-1.
La première des choses à faire est, à mon avis, de calculer les différents volumes équivalents, afin de mieux centrer la courbe.
Calcul du premier volume équivalent, noté Ve.
La réaction du dosage est:

SO2  +  HO- HSO3-
La constante de réaction Kr est égale au rapport de Ka1 sur Ke, Ke désignant la constante de l'équilibre d'autoprotolyse de l'eau.
A 25°C Kr vaut numériquement 1012. Si la cinétique le permet la réaction de dosage est quntitative car thermodynamiquement très favorisée par une constante d'équilibre Kr très supérieure à l'unité.
La réaction se faisant mole à mole entre le dioxyde de soufre dissous et l'anion hydroxyde, on aura, vu les concentrations respectives en acide et en base, une valeur numérique de 20 mL pour Ve.
Si l'on continue le dosage on aura comme réaction chimique:
HSO3-  +  HO- SO32-  +  H2O
La constante de réaction Kr de cette réaction sera égale au rapport de Ka2 sur Ke et vaudra, à 25°C,  numériquement, 2.51.106. Si la cinétique le permet, la réaction sera encore quantitative de la gauche vers la droite, puisque du point de vue thermodynamique elle est caractérisée par une constante d'équilibre très supérieure à l'unité.
Comme la réaction se fait mole à mole entre l'anion hydrogénosulfate et l'anion hydroxyde, on aura comme deuxième volume équivalent la valeur 40 mL. Il faut donc rajouter encore 20 mL aux 20 premiers mL d'hydroxyde de sodium pour neutraliser complètement le dioxyde de soufre en sulfite de disodium, plus simplement appelé sulfite de sodium, de formule Na2SO3.
Il est assez fréquent de trouver dans les livres d'exercices sur les pH des courbes qui donnent le pH en fonction non pas de V, volume de soude versé, mais en fonction du rapport sans dimension V/Ve, où V désigne le volume de soude versé et Ve le volume correspondant à la première équivalence.
Ainsi dans notre exemple, si l'on veut tracer la courbe donnant le pH en fonction de V on aura comme valeurs remarquables des abscisses les valeurs 20 mL et 40 mL, correspondant à la formation respective d'hydrogénosulfite de sodium NaHSO3 et à celle de sulfite de sodium Na2SO3.
Si au contraire on donne la courbe de pH en fonction de V/Ve on aura les valeurs remarquables d'abscisses qui seront 1 et 2 et qui correspondront respectivement à la formation d'hydrogénosulfite de sodium (première équivalence) et à celle de sulfite de sodium (deuxième équivalence).
A chacun de voir ce qui lui convient le mieux...

Pour étudier cette courbe je pense que le mieux est de la découper en trois morceaux.

Première partie: de V = 0 mL à V = 20 mL ou, si l'on préfère, de V/Ve égal à 0 à V/Ve égal à 1.
On commence par calculer les deux pH extrêmes.
La courbe de pH étant forcément strictement croissante toutes les valeurs de pH seront forcément comprises entre les deux valeurs extrêmes précédentes.
Premier calcul: calcul du pH d'une solution aqueuse de dioxyde de soufre, de concentration égale à 0.1 mol.L-1.
Vu ce qui a été vu précédemment lors du calcul des pH des solutions de diacides on pourra considérer que le dioxyde de soufre SO2 en solution aqueuse se comporte en fait comme un monoacide faible de pKa égal à pKa1, soit la valeur 2.0, à 25°C.
On appliquera la résolution de l'équation du second degré suivante:

Ka1 = 
En effet, vu la valeur particulièrement basse de pKa1, la formule magique
pH = 0,5.(pKa1 - logC0)
est ici mise en défaut.
Numériquement on trouve comme première valeur de pH pour V = 0 mL ou V/Ve = 0, la valeur:
pH = 1.57.
Deuxième calcul: calcul du pH de la solution lorsque V = 20 mL ou lorsque V/Ve = 1.
On est en présence d'une solution aqueuse d'hydrogénosulfite de sodium de concentration égale à 0.083 mol.L-1, puisque l'on doit tenir compte du facteur de dilution avec les 20 mL de soude versés dans 100 mL de solution aqueuse de dioxyde de soufre.
On est en présence d'un hydrogénosel et le pH de la solution est, dans un premier abord, indépendant de la concentration de l'hydrogénosel. On a alors comme valeur de pH la valeur donnée par la formule magique:
pH = 0,5.(pKa1  +  pKa2).
On trouve numériquement une valeur de pH pour V = 20 mL ou V/Ve = 1, la valeur pH = 4.80.
On vérifie à l'aide de la réaction prépondérante et de la réaction prépondérante secondaire si cette valeur est "bonne" ou sujette à caution. On reprend les calculs de vérification faits lors du calcul du pH des hydrogénosels et on conclut.
Ici l'approximation donnée par la formule magique des hydrogénosels est correcte. On continue...

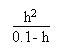
Ainsi donc entre V = 0 mL et V = 20 mL le pH de la solution variera entre 1.57 et 4.80.
Si l'on trace le diagramme de prédominance des espèces dissoutes du dioxyde de soufre en fonction du pH on voit que le dioxyde de soufre se comporte comme un monoacide faible de pKa égal à pKa1 et que la forme sulfite SO32-  est négligeable dans tous les calculs.
On peut également se rappeler que la constante Kr de la réaction de dosage

SO2  + HO- HSO3- +  H2O
est égale à 1012, ce qui fait que cette réaction est de loin la réaction prépondérante.
Ce sera elle qui imposera a priori les concentrations respectives en SO2 et HSO3- dissous.Encore faut-il qu'au départ on ait le dioxyde de soufre dissous qui soit majoritairement , pour ne pas dire essentiellement sous forme moléculaire. A défaut c'est l'équation d'électroneutralité qui donnera les concentrations respectives de SO2 et de HSO3-.
On voit bien sûr aussi que le pH sera forcément acide et que par conséquent on pourra négliger dans les calculs w devant h.
La valeur de pH correspondant à un volume V de soude versé dans les 100 mL de solution aqueuse de dioxyde de soufre sera donnée alors en toute rigueur par l'équation d'électroneutralité de la solution, qu'on résoudra.
h  +  (Na+)  =  (HSO3-)
La concentration de l'ion sodium, ion spectateur, indifférent, sera égale alors à:
(Na+) = 
La concentration de l'anion hydrogénosulfite sera égale à:
(HSO3-) = 
En remplaçant chaque terme par son expression numérique, en ne gardant bien sûr que h comme inconnue, on arrive alors à une équation du second degré qui conduit aisément au pH de la solution pour un volume V donné de soude versée dans la solution de dioxyde de soufre.

A titre d'exemple on calculera numériquement la valeur du pH lorsque le volume de soude versée est de 10 mL, bref lorsqu'on est à V/Ve qui est égal à 0.5.
L'équation du second degré à résoudre est la suivante, compte tenu des diverses valeurs numériques:

110.h2 + 6.10.h -5.10-2 = 0
On arrive à un pH de l'ordre de 2.14.
Il diffère légèrement de la valeur "tant attendue" pH = pKa1 à la demi-équivalence. C'est fréquent....Cela arrive souvent lorsque l'acide est déjà notablement dissocié au départ. C'était le cas ici, puisqu'un simple calcul à V= 0 mL de soude versé montre que le dioxyde de soufre est déjà dissocié à 26.92%. C'est dû à la valeur particulièrement basse de pKa1 et à la concentration basse elle aussi du diacide. Les deux facteurs jouant dans le même sens.
C'est ce qui a expliqué pourquoi il a fallu résoudre l'électroneutralité et non pas appliquer la formule de HENDERSON (logarithme de la constante Ka1) pour avoir accès au pH.
C'est là un écueil lorsqu'on raisonne en termes de réaction prépondérante pure et dure et qu'on oublie un énorme morceau qui est l'électroneutralité et la composition de la solution au départ.

Si je devais préférer une méthode je pencherais sans hésiter pour la résolution de l'équation d'électroneutralité dans tous les cas, plutôt que de me noyer dans certaines autres considérations qui ne sont pas applicables en toutes circonstances hélas.

Deuxième partie de la courbe maintenant: entre V = 20 mL et V = 40 mL de soude versée, soit entre V/Ve = 1 et V/Ve = 2.

L'équation du dosage devient alors:

HSO3-  +  HO-SO32-  + H2O
La constante de réaction Kr devient alors égale au rapport des deux constantes Ka2 sur Ke, soit numériquement 2.51.106. La réaction est donc quantitative de la gauche vers la droite , si la cinétique de la réaction va dans le même sens que l'aspect thermodynamique qui, lui, est favorable à la formation de l'anion sulfite.

On part d'un pH de 4.80 à V= 20 mL (soit V/Ve =1) pour arriver au pH d'une solution aqueuse de sulfite de sodium Na2SO3 de concentration égale à 0.071 mol.L-1, compte tenu des 40 mL de soude versés dans les 100 mL initiaux de solution. Le facteur de dilution n'est pas négligeable.
Le sulfite de sodium a un comportement qui s'identifie à celui d'une monobase faible dont le pKb est égal à pKb2, soit numériquement ici 6.4.On a déjà vu cela lors du calcul du pH des polybases faibles.
On essaiera d'appliquer la formule magique du pH des monobases faibles et assimilées:

pH = 7 + 0,5.(pKa2 + log )
On trouve une valeur de 10.23 pour le pH de la solution. Cette valeur étant supérieure à 8.6, c'est à dire à pKa2 + 1, on pouvait donc bien appliquer la formule magique approchée.
Entre V = 20 et V = 40 mL le pH passera donc des valeurs 4.80 à 10.23.Bref, d'acide il passera à basique et il faudra, si on résout une version simplifiée de l'équation de l'électroneutralité, faire des hypothèses sur la valeur attendue du pH. Bref un raisonnement par l'absurde ne sera pas à exclure.

On va chercher à savoir si la réaction d'amphotérisation de l'anion hydrogénosulfite est susceptible de modifier les concentrations en espèces dissoutes, par rapport aux concentrations des anions hydrogénosulfite et sulfite.
La réaction d'amphotérisation est la suivante:

2HSO3- H2SO3  +  SO32-
la valeur de la constante d'équilibre de cette réaction est égale au rapport des constantes d'acidité Ka2 sur Ka1, bref numériquement à la valeur 2.51.10-6.
En raison de la faible valeur de la constante on en déduit aisément que l'amphotérisation de l'anion hydrogénosulfite ne modifiera pas grandement les concentrations des espèces dissoutes. A ce moment là ce sera donc la réaction prépondérante qui, seule sera de nature à imposer les concentrations.
L'application de la formule de HENDERSON sera alors recommandée.
On prendra le logarithme décimal de Ka2 et l'on arrivera à:
pH = pKa2 + log 
Une question se pose: pourquoi est-ce qu'ici on peut appliquer la formule de HENDERSON et pas entre V = 0 et V = 20 mL?
C'est parce que entre V = 0 et V = 20 mL la réaction suivante :
SO2  + HO-HSO3-  + H2O
n'est pas la réaction prépondérante mais... la réaction prépondérante secondaire. La réaction prépondérante, vu que le dioxyde de soufre SO2 est déjà bien dissocié à V = 0 mL , est tout "simplement" si j'ose dire la réaction suivante:
HO-  +  H3O+ 2H2O
C'est à cause de cela qu'il a fallu résoudre l'équation de l'électroneutralité et non pas appliquer la formule de HENDERSON.

J'en conviens ce sont là des "subtilités" assez "subtiles" et j'en reviens encore une fois à plaider, malgré sa "lourdeur",  pour la résolution de l'équation de l'électroneutralité qui, elle, marche toujours...
Le seul problème c'est qu'alors ça devient peut-être beaucoup trop calculatoire....
Rien n'est parfait en ce bas monde hélas....

On pourra bien entendu comparer les résultats obtenus avec cette méthode "simplifiée" et ceux fournis par LA référence, à savoir l'équation d'électroneutralité.
Je vous en donne la forme:

h  +  (Na+)  = w  +   (HSO3-)  +  2.(SO32-)
Comme on est dans l'intervalle compris entre V = 20 mL et V = 40 mL (soit entre  V/Ve =1 et V/Ve = 2) , vu que l'amphotérisation de l'anion hydrogénosulfite est négligeable, on a affaire comme qui dirait à un monoacide HSO3- dont le pKa serait égal à pKa2.
On arrive alors à une équation du second degré dont la seule inconnue est h, tous les autres termes étant soit constants, soit des paramètres.
Pour arriver à cette équation il faut bien entendu simplifier et,  soit négliger h devant w , soit, au contraire, négliger w devant h. C'est ce que j'avais appelé la méthode par l'absurde: on postule par exemple que le pH sera acide. On raye alors w devant h. On résout et, comble de "malchance" on trouve que le pH était basique. On a alors une hypothèse de travail au départ qui est fausse. On reprend l'électroneutralité et alors on raye h devant w et on résout. Là on tombe sur un pH basique avec une hypothèse de départ d'un pH basique et ça peut tenir la route. Un raisonnement par l'absurde c'est ce "bidouillage" incessant qui est nécessaire pour tâtonner et faire avancer le Schmilblic. On peut bien sûr s'en passer. Dans ce cas il faut résoudre l'équation de l'électroneutralité de la solution en maintenant,  et h,  et w. C'est plus lourd mathématiquement  mais ça tient la route aussi.
A chacun de choisir en fonction de ses desiderata.

Si l'on choisit de résoudre l'équation de l'électroneutralité, qui marche toujours je le répète encore, il faut alors résoudre:

h  +  =  w  +  + 
Bien sûr, soit on rayera h devant w et on résoudra afin d'espérer obtenir un pH acide, soit on fera le contraire. Bref le raisonnement par l'absurde comme je vous ai dit...

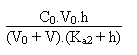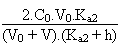
Prenons pour exemple le pH attendu lorsque V = 30 mL, bref lorsque V/Ve est égal à 1.5.
Le pH attendu est supposé être égal à 7.6, bref à la valeur pH = pKa2.
L'équation de l'électroneutralité simplifiée en fonction de cette hypothèse de pH basique devient, réarrangée en équation du second degré:

4.95.h2 -1.27.h - 3.26.10-20 = 0
On résout et on arrive, ô miracle de la Science, à pH = 7.6, CQFD!!!

On peut arriver à des résultats comparables en utilisant la relation de HENDERSON.
A ce moment là il faut juste exprimer (HSO3-) et (SO32-) en fonction des données.
On arrive alors à:

(HSO3-) = 
ainsi qu'à:
(SO32-) = 
Bref, en remplaçant par les valeurs numériques de C0, V0, Cb et Ve, à savoir respectivement: 0.1 mol.L-1, 100 mL, 0.5 mol.L-1 et 20 mL , on arrive à:
pH = 7.6 + log 
V sera exprimé en mL.
Si on remplace V par 30 mL on retombe bien sur ses pattes et on trouve que pH = pKa2, CQFD.

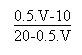
Troisième et dernière partie de la courbe de dosage: après la seconde et dernière équivalence, après V = 40 mL, soit  après V/Ve =2.
On se retrouve alors avec un excès de soude dans le milieu . La valeur asymptotique du pH tendra vers le pH de la soude de concentration égale à 0.5 mol.L-1  pour un volume V de soude versé infini.
Avant d'atteindre cette asymptote les valeurs seront comprises entre pH = 10.26 et pH =  14  + log0.5, soit 13.70,  du moins en théorie. En effet les électrodes de pH donnent ce qu'on appelle "l'erreur alcaline" pour des pH par trop basiques, supérieurs à 12. On verra cela dans un paragraphe ultérieur consacré aux électrodes.
La concentration des ions hydroxyde au delà de V = 40 mL, soit de V/Ve = 2, sera donnée par la relation:

(HO-) = 
Le pH de la solution sera donc donné par la relation:
pH = 14 + log 
A.N: si V = 60 mL, puisque Ve = 20 mL, on trouve une valeur théorique de pH, erreur alcaline mise à part, de 12.80.
On réunira les résultats sous forme de tableau.
 
Volume V de soude versée (en mL) V/Ve pH
0 0 157
10 0.5 2.14
20 1.0 4.80
30 1.5 7.60
40 2.0 10.23
60 3.0 12.80
infini infini 13.70 (attention erreur alcaline)

 Retour au plan du cours sur les pH des solutions aqueuses.

Suite du cours: cliquer ici.