Suite du cours sur les  courbes de dosage.

IV.5.b.b. Dosage de l'acide tartrique. Cas où D pKa est inférieur à 4.

 Retour au plan du cours sur les pH des solutions aqueuses.

L'acide tartrique HO2C-CHOH-CHOH-CO2H, noté "H2T" , est le principal acide du vin auquel il impose un pH compris entre 3.5 et 4.0.
Il est susceptible de donner deux équilibres acidobsiques caractérisés respectivement par deux constantes d'acidité Ka1 et Ka2, donc par conséquent, deux pKa, pKa1 et pKa2, ayant pour valeurs 3.13 et 4.31.
Par commodité dactylographique on notera l'anion hydrogénotartrate HO2C-CHOH-CHOH-CO2- par "HT-" et l'anion tartrate -O2C-CHOH-CHOH-CO2- par "T2-".
Les deux équilibres acidobasiques seront donc:

H2T  +  H2O H3O+  +  HT-
HT-  +  H2O H3O+  +  T2-
On se propose donc de calculer le pH d'une solution aqueuse d'acide tartrique de concentration C0  égale à 0.1 mol.L-1, de volume V0 égal à 100 mL, par une solution aqueuse d'hydroxyde de sodium de concentration Cb égale à 0.5 mol.L-1.
On commencera tout d'abord par cadrer la courbe de dosage entre les valeurs V = 0 mL, V = Ve mL, V = 2.Ve mL, soit les valeurs respectives de V/Ve égales à 0, à 1 et enfin à 2.
On trouve que Ve = 20 mL.
La courbe de dosage sera découpée en trois parties.
Première partie: entre V = 0 et V = Ve mL, soit entre V/Ve = 0 et V/Ve = 1.
Deuxième partie: entre V = Ve et V = 2.Ve mL, soit entre V/Ve = 1 et V/Ve = 2.
Troisième partie: au-delà de 2.Ve mL, soit au-delà de V/Ve = 2.

Première partie.
On commencera par calculer le pH initial de la solution.

On s'inspirera de ce qui a été fait pour calculer le pH d'une solution aqueuse d'un polyacide faible.
Pour une concentration d'acide tartrique égale à 0.1 mol.L-1 on a montré que l'acide tartrique adoptait un comportement de monoacide faible de pKa égal à pKa1. la seconde acidité étant négligeable devant la première. Je vous renvoie à cette partie précédente du cours "on line".

On a trouvé que le pH initial de la solution était de 2.08.

On calculera ensuite le pH de la solution lorsque V = Ve mL de soude versée, soit 20 mL ici.

L'équation du dosage est la suivante:

H2T  +  HO- HT-  +  H2O
La constante de réaction Kr est égale au rapport des constantes Ka1 sur Ke, soit, numériquement à 25°C,
7.41.1010.Si la cinétique va dans le même sens que l'aspect thermodynamique la réaction est très favorisée dans le sens gauche vers droite, c'est à dire vers la formation de l'anion hydrogénotartrate, ce que l'on constate d'ailleurs expérimentalement.
A V = 20 mL, ou V/Ve = 1, on se retrouve avec une solution aqueuse d'hydrogénotartrate de sodium NaHT de concentration égale à 0.083 mol.L-1, en raison du facteur de dilution introduit par l'ajout des 20 mL de soude dans le volume initial de la solution.
L'hydrogénotartrate de sodium NaHT est un hydrogénosel et son pH est a priori indépendant de la concentration.
Il subit la réaction d'amphotérisation classique suivante:
2HT- H2T  +  T2-
La constante d'équilibre de cette réaction est égale au rapport des deux constantes d'acidité Ka2 sur Ka1 et vaut numériquement, à 25°C, 0.066.
On a en première approche la possibilité d'appliquer la formule magique suivante, classique des hydrogénosels:
pH = 0,5.(pKa1 + pKa2)
Numériquement cela ferait ici un pH de 3.72.

On pourra vérifier que l'anion hydrogénotartrate ne subit pas d'hydrolyse  en anion tartrate et ion hydronium, ou plutôt que cette hydrolyse, caractérisée par la constante d'équilibre Ka2, est négligeable devant la réaction d'amphotérisation. Cette vérification a été faite dans la partie sur les hydrogénosels que j'ai traitée plus haut.Il faut faire un tableau avec les valeurs des concentrations des espèces dissoutes "avant" et "après" puis résoudre en fin de compte une équation du second degré.

Le pH imposé alors par la réaction d'amphotérisation est bien égal à 3.72, ce que donnait la formule magique.

Que vaut le pH de la solution pour un volume de soude versé égal par exemple à 10 mL?
L'équation complète de l'électroneutralité de la solution s'écrit:

h  + (Na+)  =  w  + (HT-)  +  2.(T2-)
Comme le pH sera acide (vu qu'on se situe entre pH = 2.08 et pH = 3.72) pour un volume V = 10 mL de soude versée, on pourra négliger w devant h.
La réaction du dosage est la suivante:
H2T  +  HO-  HT-  +  H2O
La valeur de la constante de réaction a été calculée plus haut et montre que la réaction est thermodynamiquement très favorisée.
Est-ce que cette réaction est la seule qui impose les concentrations des diverses espèces dissoutes ou bien faut-il rechercher une autre réaction?
La réaction qui vient à l'esprit est celle de l'amphotérisation de l'anion hydrogénotartrate formé par action de l'anion hydroxyde sur la molécule d'acide tartrique H2T.
2HT- H2T  +  T2-
La constante de cet équilibre d'amphotérisation a une valeur de 0.066 à 25°C.
Or, déjà à V = 0 mL, avec un pH égal à 2.08 on avait un taux de dissociation de l'acide tartrique qui valait 8.32%. Ce taux n'est pas complètement négligeable.
La réaction prépondérante sera, encore une fois, non pas la réaction entre les molécules d'acide tartrique et les ions hydroxyde mais bien celle entre les ions hydronium et les ions hydroxyde.
On considèrera alors que l'acide tartrique se comporte comme un monoacide faible de pKa égal à pKa1, on résoudra l'équation de l'électroneutralité en négligeant dans un premier temps le terme (T2-) puis, après ce calcul on reprendra encore la réaction d'amphotérisation et on cherchera à savoir  si elle "perturbe" ou non les résultats de la méthode simplifiée.

On cherchera donc, dans un premier temps, à résoudre l'équation suivante:

h  +  (Na+)  =  (HT-)
Pour un volume V de soude versée égal à 10 mL on a (Na+) qui vaut 0.045 mol.L-1.
(HT-) = 
Numériquement en remplaçant C0, V0,V,  Ka1 par leurs valeurs et en recollant les morceaux on arrive à l'équation du second degré suivante:
110.h2  +  5.03.h  -3.74.10-3  =  0
On trouve une valeur de pH égale à 3.14, donc pratiquement égale à pKa1.
Cette valeur de pH impose alors les concentrations en H2T et HT-.
On écrira la conservation de la matière:
(H2T)  +  (HT-)  = 0.083 mol.L-1
On introduira la constante d'acidité Ka1. On connaît sa valeur numérique, on connaît le pH, on exprime (H2T) en fonction de (HT-) à l'aide de l'équation de conservation de la matière et on arrive à:
(H2T) = (HT-) = 0.042 mol.L-1.
On regardera maintenant l'influence éventuelle de la réaction d'amphotérisation sur ces concentrations calculées de façon simplifiée.

On fera un tableau afin de préciser les concentrations des diverses espèces dissoutes "avant" et "après" l'instauration de tous les équilibres possibles, censés s'instaurer dans le milieu.
Les données sont fournies en mol de substance dissoute  par litre de solution.
 

HT- H2T T2-
Avant instauration de l'équilibre d'amphotérisation. 0.042  0.042  0
Après instauration de l'équilibre d'amphotérisation 0.042 - 2.x 0.042 + x x

Il faut alors résoudre l'équation du second degré obtenue d'après:

Kamphotérisation = 0.066 = 
0.736.x2  +  5.31.10-2.x  -1.16.10-4  =  0.
On résout et on trouve que x = 2.12.10-3.
On en déduit que les concentrations en diverses espèces dissoutes deviennent:
 
(H2T) 4.41.10-2 mol.L-1
(HT-)  3.78.10-2 mol.L-1
(T2-)  2.12.10-3 mol.L-1

On vérifie que la somme des trois concentrations est bien égale à 0.083 mol.L-1, aux erreurs d'arrondi près.
En appliquant désormais les expressions des constantes d'acidité, soit Ka1 soit Ka2 au choix, on arrive à trouver h, donc le pH, connaissant Ka1, ou Ka2, (H2T), (HT-) et (T2-).
A vec Ka1 on arive à pH = 3.06.
Avec la méthode simplifiée on avait trouvé pH = 3.14.
Comme les calculs de pH ne tolèrent qu'une erreur de 0.05 entre deux méthodes distinctes  on considèrera qu'on était en droit d'appliquer une méthode plus complète afin de trouver le pH à V = 10 mL, soit à V/Ve = 0.5.

Cette méthode sera à appliquer pour tous les points compris entre V = 0 mL et V = 20 mL.
Elle sera plus ou moins "utile" cela dépendra des valeurs de V.

Deuxième partie de la courbe: entre V = 20 et V = 40 mL, soit entre V/Ve = 1 et V/Ve = 2.
La réaction du dosage est alors:

HT-  +  HO- T2-  +  H2O
La valeur de la constante de réaction Kr est égale au rapport de Ka2 sur Ke, soit numériquement à 25°C 4.90.109.
C'est encore une fois du point de vue thermodynamique une valeur très favorable à la formation de l'anion tartrate. La cinétique allant en ce sens aussi c'est ce qu'on observe expérimentalement.

On calculera la valeur extrême  du pH lorsque V = 40 mL, soit lorsque V/Ve = 2.
On se retrouve avec une solution de tartrate de sodium Na2T de concentration égale à 0.071 mol.L-1 en raison du facteur de dilution introduit par les 40 mL de soude versés dans les 100 mL de solution.
On appliquera la formule magique suivante:

pH = 7 + 0,5.(pKa2 + log )
En remplaçant les termes par leur expression numérique on arrive à un pH de 8.58.
Cette valeur de pH étant largement supérieure à 5.31, soit à pKa2 + 1, la formule magique est suffisante et surtout applicable pour le calcul du pH considéré.

Que vaut le pH de la solution lorsqu'on a versé un volume V de soude égal à 30 mL par exemple?
On est alors à V/Ve = 1.5.
Dans un premier temps on calculera les concentrations en HT- et T2- à l'aide de la réaction:

HT-  +  HO- T2-  +  H2O
Il y avait au départ 0.01 mol d'acide tartrique transformé en 0.01 mol d'anions hydrogénotartrate à V = 20 mL. Après ajout de 10 mL de soude supplémentaires, c'est à dire pour un volume V total de soude versée de 30 mL, il s'est formé 0.005 mol d'anions tartrate et il reste 0.005 mol d'anions hydrogénotartrate.
La concentration de ces espèces vaut alors: 0.0385 mol.L-1.
On étudiera alors l'influence de la réaction d'amphotérisation sur ces concentrations.
2HT- H2T  +  T2-
Les concentrations sont exprimées en mol.L-1.
HT- H2T T2-
Avant instauration de l'équilibre d'amphotérisation 0.0385 0 0.0385
Après instauration de l'équilibre d'amphotérisation 0.0385-2.x x 0.0385 +x
On en arrive à devoir résoudre l'équation du second degré suivante, sachant que la valeur de la constante d'équilibre d'amphotérisation vaut 0.066 à 25°C:
0.736.x2  +  4.87.10-2.x  -  9.78.10-5  =  0
On arrive à une valeur de x égale à 1.95.10-3.
Les concentrations, exprimées en mol.L-1,  des diverses espèces dissoutes deviennent alors:
 
H2T 1.95.10-3
HT- 4.045.10-2
T2- 3.46.10-2

On vérifie, aux erreurs d'arrondi près, que la somme des trois concentrations fait bien 0.077 mol.L-1, concentration lorsque V = 30 mL de soude versée dans les 100 mL de solution d'acide tartrique.
On peut dès lors, à l'aide des constantes d'acidité Ka1 ou Ka2, remonter à la valeur du pH de la solution  à v = 30 mL.
On trouve que le pH vaut 4.24.

On recommencera ainsi pour toutes les valeurs comprises entre V/Ve = 1 et V/Ve = 2.

Troisième partie de la courbe: après V = 40 mL, soit après V/Ve = 2.
On est alors en présence d'un excès de soude. C'est cet excès qui imposera le pH de la solution.
On calculera le pH de la solution lorsque le volume V  de soude versé est égal à 50 mL, bref lorsqu'on se situe à V/Ve = 2.5.
Le pH de la solution sera donné, tout comme pour le cas du dioxyde de soufre en solution aqueuse (exemple précédent), par la formule:

pH = 14 + log 
On trouve une valeur de 12.52.
Le pH tendra en théorie asymptotiquement vers la valeur du pH de la soude, soit 13.70, l'erreur alcaline ramenant en fait le pH vers 12.
On résumera les résultats sous forme d'un tableau.
 
Volume V de soude versée (en mL) V/Ve pH
0 0 2.08
10 0.5 3.06 (et non 3.13)
20 1.0 3.72
30 1.5 4.24 (et non 4.31)
40 2.0 8.58
50 2.5 12.52
infini infini 13.70 (attention erreur alcaline)

 Retour au plan du cours sur les pH des solutions aqueuses.

IV.5.b.g. Cas du dosage d'un diacide idéal.

 Retour au plan du cours sur les pH des solutions aqueuses.

Les deux exemples précédents illustrent bien le fait  qu' hormis la résolution de l'équation de l'électroneutralité sous sa forme complète il n'y a guère de méthode simple,  ou plutôt généralisable à l'infini, pour calculer tous les points d'une courbe de dosage.
Tantôt la relation d'HENDERSON s'applique, tantôt elle ne s'applique pas.
Tantôt on a pH = pKa à la demi-équivalence, tantôt on ne l'a pas. Etc....
Tout cela dépend en fait de deux facteurs: la valeur de la concentration initiale de l'acide et les valeurs respectives des deux pKa de l'acide.
Je vous donne, à titre d'exemple, ou plutôt à titre de conte de fée, le cas d'un diacide idéal qui aurait le mérite de donner des calculs simples pour chaque partie de sa courbe de dosage.
La courbe est toujours découpée en trois parties.

Première partie: entre V/Ve = 0 et V/Ve = 1.
Pour V  = 0 le pH idéal est calculé à l'aide de la formule magique:

pH = 0,5.(pKa1 - log C0).
Pour V = 0.5.Ve le pH est égal à pKa1.
Pour V = Ve le pH est calculé à l'aide de la formule magique:
pH = 0,5.(pKa1 + pKa2).

Deuxième partie: entre V/Ve = 1 et V/Ve = 2.
Pour V/Ve = 1.5 le pH est égal à pKa2.
Pour V/Ve = 2 le pH est donné par la formule magique:

pH = 7 + 0,5.(pKa2 + log )

Troisième partie: au-delà de V/Ve = 2.
Le pH est donné par la formule:

pH = 14 + log 
On voit bien que dans les cas réels on "oscille" avec ces formules magiques: tantôt on peut s'en servir et tantôt pas.
La partie qui souvent pose problème est souvent la première, celle comprise entre V/Ve = 0 et V/Ve = 1.
Souvent le diacide a un premier pKa qui est petit et, si en plus la concentration de l'acide est faible, alors on n'atteint jamais la valeur pH = pKa1 à la première demi-équivalence.
Par rapport aux cours de Terminale sur les pH je trouve que c'est là pour vous une grande nouveauté.
Il faut se méfier toujours des formules par trop "magiques" c'est à dire non redémontrées à chaque fois.
Chaque cas étant en fait un cas particulier.
Incredible but... true!

Je ne saurais trop vous recommander, dans la mesure du possible, de toujours faire les manips vous mêmes avant de vous lancer dans des calculs qui peuvent sembler par trop délirants.
L'expérience c'est ça qui est déterminant.
La chimie n'étant pas une science exacte mais expérimentale il faut toujours se raccrocher à l'expérience.
Les modélisations par trop mathématiques ça ne marche pas toujours.
On peut le regretter mais c'est ainsi.
Ces exercices n'ont pour d'autre but que de vous "amuser" (!!!!) et ne sont pas faits pour vous dégoûter à jamais des pH. Loin de là!
Un de mes meilleurs profs de chimie, un certain JPB de l' université de  Bordeaux I ,  disait toujours: "Les pbs de pH ça n'existe pas. Il faut juste  tremper l'électrode et on lit."
Il avait bien raison Jean-Pierre, oui, il avait bien raison....

 Retour au plan du cours

IV.5.b.d.Dosage d'un triacide faible, l'acide phosphorique. Cas où D pKa est supérieur à 4.

 Retour au plan du cours sur les pH des solutions aqueuses.

On cherchera à calculer le pH des différents points de la courbe de dosage de 100 mL  d'une solution aqueuse d'acide phosphorique, triacide faible minéral de formule H3PO4, de concentration C0 égale à 0.1 mol.L-1 par une solution aqueuse d'hydroxyde de sodium de concentration égale à 0.5 mol.L-1.Les valeurs respectives des trois pKa de l'acide phosphorique valant à 25°C 2.15, 7.20 et 12.10.

Comme d'habitude,  désormais,  on commencera par scinder la future courbe de dosage en quatre parties:
Première partie: de V/Ve = 0 à V/Ve = 1.
Deuxième partie: de V/Ve = 1 à V/Ve = 2.
Troisième partie: de V/Ve = 2 à V/Ve = 3.
Quatrième et dernière partie: au-delà de V/Ve = 3.

Dans l'exemple qui est choisi on aura Ve qui sera égal à 20 mL. C'est le volume de soude qu'il faut verser dans les 100 mL de solution initiale pour obtenir la première équivalence acidobasique, celle qui donne le premier des hydrogénosels de l'acide phosphorique le dihydrogénophosphate de sodium, de formule NaH2PO4.Sa concentration sera alors égale, compte tenu du facteur de dilution,  à 0.083 mol.L-1.

La seconde équivalence, pour V = 40 mL correspondra à la formation du deuxième hydrogénosel de l'acide phosphorique le monohydrogénophosphate de disodium, plus communément appelé hydrogénophosphate de sodium, de formule Na2HPO4, de concentration égale à 0.071 mol.L-1, en raison du facteur de dilution.

La troisième équivalence, pour V = 60 mL correspondra à la formation de phosphate de trisodium, plus communément appelé phosphate de sodium, de formule Na3PO4 et de concentration, compte tenu du facteur de dilution, égale à  0.0625 mol.L-1.

Au-delà de la troisième équivalence on aura un excès de soude en présence de phosphate de sodium.

Première partie: entre V = 0 et V = Ve = 20 mL, soit entre V/Ve = 0 et V/Ve = 1.
Le pH initial sera celui d'une solution d'un polyacide faible qui se comportera en fait comme un monoacide faible de pKa égal à pKa1.
On ne pourra pas appliquer la formule magique suivante:

pH = 0,5.(pKa1 - log C0)
Le pH qu'elle fournit est de 1.58, valeur qui n'est pas inférieure à pKa1 - 1.
On résoudra en conséquence le trinôme suivant:
h2 + 7.08.10-3.h - 7.08.10-4 = 0
On arrive à un pH de 1.63.
Le degré de dissociation a correspondant est de 23.44%.
L'acide phosphorique, du fait d'un premier pKa relativement bas est déjà fortement dissocié au départ.

Calculons le pH lorsqu'on est à V = 20 mL.
On a atteint alors la première équivalence.
On a une solution de dihydrogénophosphate de sodium NaH2PO4  de concentration égale à 0.083 mol.L-1.Comme c'est un hydrogénosel on cherchera à appliquer tout d'abord la formule magique suivante:

pH = 0,5.(pKa1 + pKa2)
La valeur attendue est alors la suivante: pH = 4.68.
La réaction d'amphotérisation est la suivante:
2H2PO4- H3PO4 + HPO42-
La valeur de la constante d'équilibre de cette réaction est égale au rapport de Ka2 sur Ka1.
Numériquement cela vaut 8.91.10-6
Cette réaction impose dans un premier temps les concentrations dans les trois espèces dissoutes précédentes.
On doit résoudre l'équation suivante:
8.91.10-6 = 
On trouve que x = 2.48.10-4.

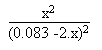
On regarde maintenant si la réaction d'hydrolyse de l'anion dihydrogénophosphate en hydrogénophosphate est de nature à modifier le pH fourni par la formule magique des hydrogénosels.
La réaction est la suivante:

H2PO4-  +  H2O HPO42- + H3O+
La constante d'équilibre est égale à pKa2, soit numériquement 6.31.10-8 à 25°C.
On dressera un tableau qui spécifiera les concentrations, exprimées en mol.L-1, de chacune des espèces dissoutes, avant et après instauration de cet équilibre acidobasique.
 
H2PO4- H3O+ HPO42-
Avant instauration de l'équilibre d'hydrolyse acide de l'anion dihydrogénophosphate 0.0825 = 
0.083 -2.2,48.10-4		 0 2.48.10-4
Après instauration de l'équilibre acidobasique 0.0825 - x x 2.48.10-4 + x
On doit alors résoudre encore une fois une équation du second degré:
6.31.10-8 = 
L'équation du second degré qui est obtenue après réarrangement est la suivante:
x2 + 2.48.10-4.x - 5.20.10-9 = 0
On arrive à une valeur de x qui vaut 1.95.10-5.Le pH est alors de 4.71.
Cette valeur de pH différant de moins de 0.05 de la valeur donnée par l'application de la formule magique des hydrogénosels on considèrera que le pH de la solution n'est pas modifié par la réaction d'hydrolyse, au demeurant négligeable, de l'anion digydrogénophosphate en hydrogénophosphate.
Le pH à V = 20 mL, soit V/Ve = 1, est donc considéré comme égal à 4.68.

Que vaut le pH de la solution lorsque V= 10 mL, bref lorsqu'on est à V/Ve = 0.5?

Il y a tout lieu de s'attendre à une valeur de pH qui sera proche de pKa1, voire égale à pKa1. L'équation complète de l'électroneutralité de la solution, à savoir:

h + (Na+) = w + (H2PO4-) + 2.(HPO42-) + 3.(PO43-)
a tout lieu de se simplifier en:
h + (Na+) =   (H2PO4-)
En effet, h est plus grand que w à cet endroit, et l'acide phosphorique se comporte comme un monoacide faible de pKa égal à pKa1.
La réaction prépondérante au voisinage de V/Ve = 0.5 est la réaction entre les ions hydronium provenant de la dissociation de l'acide phosphorique et les ions hydroxyde versés par la soude.On n'oubliera pas que déjà à V/Ve = 0 on avait un degré de dissociation de l'acide phosphorique qui était de l'ordre de 23 % à la concentration de 0.1 mol.L-1.

La réaction prépondérante secondaire est l'action des ions hydroxyde sur la molécule d'acide phosphorique, conduisant à l'anion dihydrogénophosphate.

On aura à résoudre une équation du second degré obtenue après avoir donné leur expression numérique à chacun des termes de l'expression littérale de l'électroneutralité.
On a:

(Na+) = 
(H2PO4-) = 
On arrive alors à l'équation du second degré suivante:
h2 + 5.21.10-2.h  -3.25.10-4 = 0
Le pH trouvé est de 2.25.

Si l'on veut  généraliser ce mode de calcul on est amené à devoir résoudre l'équation du second degré suivante pour toute valeur de V comprise ente V = 0 et V = 20 mL.

(V0 + V).h2 + h.[Cb.V + Ka1.(V0 + V)] + Ka1.[Cb.V -C0.V0] = 0

Deuxième partie: calcul du pH des points de la courbe entre V/Ve = 1 et V/Ve = 2.

Lorsque V/Ve = 1 on a un pH de 4.68.

Lorsque V/Ve = 2 on est en présence d'une solution aqueuse d' hydrogénophosphate de disodium Na2HPO4 , de concentration égale à 0.071 mol.L-1.

La réaction prépondérante est la réaction entre les ions hydroxyde apportés par la soude et les ions dihydrogénophosphate:

H2PO4- + HO- HPO42- + H2O
La constante de réaction Kr est égale au rapport de Ka2 sur Ke. Numériquement elle vaut, à 25°C, 6.31.106.
Le pH de la solution d'hydrogénophosphate de disodium Na2HPO4 de concentration égale à 0.071 mol.L-1 est donné dans un premier temps par la formule magique:
pH = 0,5.(pKa2 + pKa3)
soit, numériquement 9.65 à 25°C.Cette formule correspond à une valeur de pH calculée uniquement d'après la réaction d'amphotérisation de l'anion hydrogénophosphate en dihydrogénophosphate et phosphate:
2HPO42-H2PO4- + PO43-
Cette réaction d'amphotérisation a pour constante d'équilibre le rapport de Ka3 sur Ka2, soit numériquement à 25°C 1.26.10-5.
Il faut alors vérifier si l'anion hydrogénophosphate est susceptible ou non de donner une réaction d'hydrolyse .

On reprend la même méthode que pour le premier des hydrogénosels de l'acide phosphorique, à savoir le dihydrogénophosphate de sodium NaH2PO4 et l'on constate qu'on arrive à un pH de 9.65. C'est la valeur trouvée également en appliquant la formule magique des hydrogénosels. On en déduit que l'hydrogénophosphate de disodium Na2HPO4 est un pur hydrogénosel et qu'il ne conduit pas à une hydrolyse partielle susceptible de modifier la valeur du pH de la solution.

On constate encore une fois que le pH de l'hydrogénosel à cette concentration est indépendant de sa concentration.

Entre V/Ve = 1 et V/Ve = 2, bref pour des volumes de soude versés compris entre 20 et 40 mL, le pH de la solution étudiée variera de 4.68 à 9.65.

Que vaut le pH de la solution lorsque V/Ve = 1.5, bref lorsqu'on a versé 30 mL de soude dans 100 mL de solution d'acide phosphorique?

Il faut revenir à l'électroneutralité de la solution.
Vu que le pH sera de toute façon inférieur à 9.65 on peut, d'ores et déjà, négliger le terme en phosphate dans l'équation d'électroneutralité.
Celle ci s'écrira dès lors:

h + (Na+) =  w + (H2PO4-) + 2.(HPO42-)
Dans cette zone l'acide phosphorique n'interviendra qu'avec son  pKa2.Cela est montré en tenant compte du diagramme de prédominance des espèces dissoutes entre les deux valeurs extêmes de pH. la forme moléculaire y est négligeable tout comme la forme phosphate.
Il ne se pose que la question des valeurs respectives de h devant w.
Je préconise que l'on reprenne les raisonnements par l'absurde à chaque fois, si l'on veut éviter de se traîner et h, et w.
Je rappelle que raisonner par l'absurde c'est par exemple postuler que le pH de la solution, pour un volume V de soude versé, sera acide. Dans ce cas il vient sans problème que dans l'équation d'électroneutralité on garde h devant w et donc qu'on raye ce dernier. Si en faisant cette hypothèse on tombe sur une valeur de h donnant un pH basique c'est alors que l'hypothèse de départ était fausse. On reprend l'électroneutralité et alors on garde w devant h, h qu'on raye alors.On recalcule alors la valeur de h solution de l'équation et, bien entendu, on tombe alors sur un pH basique, ce qui est en accord avec l'hypothèse de départ.
On aura alors:
(Na+) = 
(H2PO4-) = 
2.(HPO42-) = 
A partir de là il ne reste plus qu'à résoudre.
Si l'on postule que pour V = 30 mL le pH de la solution sera basique  (comme qui dirait égal à pKa2) on arrive à l'équation du second degré suivante, en ayant au préalable remplacé chacun des termes par sa valeur numérique:
4.95.h2 -3.17.10-7.h -8.20.10-20 = 0
On arrive à pH = 7.20. C'est égal au pKa2 de l'acide phosphorique.
Si bien entendu on était parti de l'idée que le pH serait acide on serait tombé sur une valeur de pH qui aurait été basique et alors il aurait fallu reprendre les calculs en modifiant dans l'équation d'électroneutralité l'hypothèse de départ.

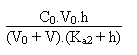
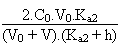
Troisième partie: entre V/Ve = 2 et V/Ve = 3.

Lorsque V/Ve = 3 on se retrouve avec une solution aqueuse de phosphate de trisodium Na3PO4, plus communément appelé phosphate de sodium, de concentration égale à 0.0625 mol.L-1.
Le pH de la solution sera donné en faisant intervenir la constante Kb3 de l'acide phosphorique.Sa valeur numérique est égale, à 25°C, à 1.26.10-2.Le phosphate de sodium, tribase faible, se comporte en fait comme une monobase faible de pKb égal à pKb2, soit numériquement 1.90.L'équation de second degré en wqu'on obtient est alors la suivante:

w2 + 1.26.10-2.w -7.88.10-4 = 0
La résolution conduit alors à un pH de 12.35.
Dans la troisième partie de la courbe, entre V/Ve = 2 et V/Ve = 3, le pH de la solution variera entre 9.65 et 12.35.
La réaction de dosage sera la suivante:
HPO42- + HO- PO43- + H2O
La valeur de la constante de réaction Kr sera égale au rapport de Ka3 sur Ke, soit numériquement 79.43 à 25°C.Ce n'est pas une valeur suffisamment élevée pour qu'on puisse considérer la réaction comme totale de la gauche vers la droite. En raison de cela on ne pourra pas faire intervenir l'approximation de HENDERSON. Les ions hydroxyde devront dès lors figurer dans l'équation d'électroneutralité et ne pourront pas être négligés inconsidérément devant les autres concentrations des espèces dissoutes en présence dans le milieu.

Si l'on veut calculer le pH de la solution en un point quelconque de la courbe compris dans cet intervalle il faudra résoudre l'équation d'électroneutralité qui aura la forme suivante:

(Na+) = w + 2.(HPO42-) + 3.(PO43-)
L'acide phosphorique dans cette zone se comportera comme un monoacide faible de pKa égal à pKa3.
L'équation d'électroneutralité s'écrira dès lors:
(Na+) = w + +
Cherchons par exemple à calculer le pH de la solution pour V/Ve = 2.5, soit pour un volume de soude versé égal à 50 mL.
En remplaçant chacun des termes de l'équation par son expression numérique on arrive à une équation du second degré qui est:
5.05.h2 -5.43.10-2.h -1.19.10-24 = 0
Le pH est alors de 11.90.

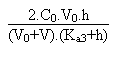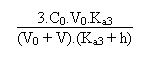
Si l'on avait choisi un volume de soude versée V quelconque,  mais compris entre 40 et 60 mL, on aurait eu à résoudre l'équation du second degré suivante:

[2.C0V0-Cb.V].h2 + [Ke.(V0+V) -Cb.V.Ka3 + 3.C0.V0.Ka3].h + Ka3.Ke.(V0+V) = 0

Quatrième et dernière partie: au-delà de V/Ve = 3.

Que vaut le pH de la solution lorsque le volume V de soude versée est de 70 mL?

On est alors en présence d'un excès de soude et de phosphate de trisodium. C'est l'excès de soude, base forte, qui imposera le pH de la solution.
Le pH de la solution sera donné par la formule:

pH = 14 + log 
On trouve pour V = 70 mL une valeur de pH qui est de 12.47.
On récapitulera les résultats des valeurs de pH des principaux points de la courbe de dosage de l'acide phosphorique par la soude dans un tableau.
 
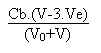
Volume V de soude versée (mL) V/Ve pH
0 0 1.67
10 0.5 2.25 (et non pas 2.15, valeur de pKa1)
20 1.0 4.68
30 1.5 7.20 (pKa2)
40 2.0 9.65
50 2.5 11.90 (et non pas 12.10, pKa3)
60 3.0 12.35
70 3.5 12.47
infini infini 13.70(attention erreur alcaline)

 

 Retour au plan du cours sur les pH des solutions aqueuses.

Pour obtenir la suite cliquez ici.