Retour au plan du cours sur les pH des solutions aqueuses.
Chapitre I: le solvant eau.
Exercice I.1.
1. La densité d d'un liquide est le rapport, à
une température et à une pression données, de la masse
volumique r de ce liquide sur la masse
volumique r de l'eau.
Exemple: lorsqu'on dit que la densité de l'huile
est de 0.85 cela veut dire que la masse volumique r
de l'huile est égale à 0.85 g.cm-3 et qu'on a
divisé cette valeur par celle de l'eau, à savoir 1.00 g.cm-3.
La densité d'un liquide n'a pas d'unités.
2. La densité d'un solide est égale au rapport
de la masse volumique r de ce solide,
à T et P données, sur celle de l'eau.
Lorsqu'on dit que la densité du platine est de
21.5 cela veut donc dire que la masse volumique du platine est égale
à 21.5 g.cm-3, et qu'on a divisé cette valeur
par celle de l'eau, prise comme référence.
La densité d'un solide n'a pas d'unités.
3. la densité d'un gaz est égale au rapport
de la masse d'un volume V de ce gaz, pris à T et V données,
sur la masse d'un même volume d'air, pris à T et P données.
Si le volume est égal au volume molaire (22.4
L dans les conditions dites normales de température et de pression:
i.e. P = 1.013 bar et T = 273 K) alors la masse de 22.4 L d'air sera égale,
si l'on admet que l'air est composé à 80 % de diazote et
à 20 % de dioxygène, à 29 g.
On aura alors la relation:
d = M/29, où M désigne la masse molaire
du gaz. La densité d'un gaz n'a pas d'unités.
La densité du gaz dihydrogène H2
sera alors égale à 2/29 soit à 0.069 environ. Il sera
donc moins dense que l'air.
Celle du gaz dichlore Cl2 sera alors égale
à 71/29 soit à 2.45. Il sera donc plus dense que l'air.
4. Le fait que la densité d de l'acide sulfurique
fasse 1.86 signifie que si l'on prend un litre de cette solution la masse
correspondante sera égale à 1.86 kg.
Cela signifiera que la masse volumique r
de l'acide sulfurique sera égale à 1.86 kg.dm-3.
5. la réponse est donnée déjà au 4.
6. La masse volumique r de l'acide sulfurique sera égale à 1.86 g.cm-3, à 1.86 g.mL-1, à 1860 kg.m-3, à 1.86 t.m-3, à 1860 mg.mL-1, à 1.86 µg.µL-1.
7. Masse volumique et densité sont mesurées
par les mêmes chiffres mais attention!!!! la masse volumique
a une unité et pas la densité.
Ecrire que la densité du platine est de 21.5 g.cm-3
est une grave faute.
Exercice I.2.
1. Dans 250 mL de solution à 0.01 mol.L-1
il y a 2.50.10-3 mol de HA.
Pour avoir ce nombre de moles à partir d'une solution
de HA à 0.1 mol.L-1 il faut prélever 25 mL.
2. Dans 50 mL de HA à 0.1 mol.L-1 il
y a 5.10-3 mol de HA.
Dans 125 mL de HA à 0.25 mol.L-1 il
y a 3.125.10-2 mol de HA.
Dans 125 + 50 = 175 mL de mélange il y aura 3.625.10-2
mol de HA.
La concentration de HA dans le mélange sera égale
à 0.207 mol.L-1.
3. Dans 50 mL de HA à 0.01 mol.L-1 il
y a 5.10-4 mol de HA.
Dans 1000 mL de HA à 0.1 mol.L-1 il
y a 0.1 mol de HA.
Dans 1000 + 50 = 1050 mL de mélange il y a 0.1005
mol de HA.
La concentration de HA sera égale à 0.0957
mol.L-1.
Exercice I.3.
1. Dans 1 mL de HCl à 32% en masse il y a une masse
de 0,32.1.16 g de HCl. Soit: 0,3712 g. Soit, vu que la masse molaire de
HCl est égale à 36.5 g.mol-1, 1.017.10-2
mol de HCl.
Si l'on prend 9.83 mL de la solution concentrée
et qu'on étend à 1000 mL alors on a une solution qui est
à 0.1 mol.L-1.
Comme 9.83 mL sont "impipetables" on prélèvera
tout simplement 10 mL de la solution concentrée et on étendra
à 1000 mL. La concentration de l'acide ne sera désormais
plus égale à 0.1 mol.L-1 exactement mais aura
la valeur de 0.1017 mol.L-1.
2. Dans 1 mL de solution concentrée il y a 1.017.10-2 mol de HCl. Si on rajoute 50 mL d'eau le volume sera de 51 mL. La concentration en acide sera égale à 0.199 mol.L-1.
Exercice I.4.
1. Dans 1 mL de NH3 à 20 % et de densité
0.92 il y a 0,20.0,92 g de NH3. Soit 0,184 g de NH3.Soit
1.08.10-2 mol de NH3.
Si l'on prélève 9.26 mL de NH3
concentré et qu'on étend à 1000 mL on a réalisé
une solution à 0.1 mol.L-1. Mais comme 9.26 mL sont encore
une fois "impipetables" on choisit tout simplement de pipeter 10 mL de
solution concentrée et d'étendre à 1000 mL. La concentration
de la solution est alors égale à 0,108 mol.L-1.
2. Dans 1 mL de NH3 concentré il y a 1.08.10-2 mol de NH3. Si l'on rajoute 50 mL on a un volume total de 51 mL. La concentration de NH3 devient alors égale à 0,212 mol.L-1.
Exercice I.5.
1. La masse molaire de l'acide oxalique dihydraté
cristallisé est égale à 126 g.mol-1.
Dans 126 g de cristaux il y a une mole d'acide oxalique.
Dans 12.6 g il y a 0.1 mol d'acide.
Dans 6.3 g de cristaux il y a 0.05 mol d'acide oxalique.
Si on dissout 6.3 g de cristaux dans une fiole jaugée
de 500 mL et qu'on étend la dissolution à 500 mL alors on
aura réalisé une solution aqueuse d'acide oxalique à
0.1 mol.L-1.
2. 3,00 g de cristaux correspondent à 2.38.10-2
mol d'acide oxalique.
Dans 500 mL de solution il y aura alors 2.38.10-2
+ 0.05 = 7.38.10-2 mol d'acide oxalique. La concentration en
cet acide sera devenue égale à 0.1476 mol.L-1.
Chapitre II. Les acides et les bases. Les pH des solutions simples.
Exercice II.1.
1. Le pH valant 3.15 la concentration des ions hydronium
est égale à 7.08.10-4 mol.L-1.
La concentration des ions hydroxyde vaut alors 1.41.10-11
mol.L-1.
La concentration des ions éthanoate vaut alors
7.08.10-4 mol.L-1.
La concentration de l'acide non dissocié
vaut 2.82.10-2 mol.L-1.
2. La concentration C de l'acide éthanoïque dissous est alors égale à 2.82.10-2 + 7.08.10-4 = 2.89.10-2 mol.L-1.
3. Le degré de dissociation a de l'acide éthanoïque est égal à 2.45 %.
Exercice II.2.
1. Le pH de la solution aqueuse d'acide éthanoïque est égal à 2.94.
2. La concentration des ions hydronium est égale
à 1.15.10-3 mol.L-1.
La concentration des ions hydroxyde est égale
à 8.71.10-12 mol.L-1.
La concentration des ions éthanoate est égale
à 1.15.10-3 mol.L-1.
La concentration en acide éthanoïque non
dissocié est égale à 7.385.10-2 mol.L-1.
3. Le degré de dissociation a de l'acide éthanoïque est égal à 1.53 %.
4. La concentration de l'acide éthanoïque
après mélange vaut 0.025 mol.L-1.
Le pH de la solution vaut alors: 3.18.
La concentration des ions hydronium vaut alors 6.67.10-4
mol.L-1.
La concentration des ions hydroxyde vaut 1.50.10-11
mol.L-1.
La concentration des ions éthanoate vaut 6.67.10-4
mol.L-1.
La concentration en acide éthanoïque moléculaire,
non dissocié est égale à 2.43.10-2 mol.L-1.
Le degré de dissociation a
de
l'acide éthanoïque vaut alors 2.64 %.
C'est normal que le degré de dissociation a
augmente avec la dissolution puisque le pH augmente.Voir le diagramme de
prédominance de l'acide éthanoïque.
Exercice II. 3.
1. Si l'acide était fort son pH serait de 1.30. Il est de 3.50 donc il est faible.
2. Son Ka vaut 2.01.10-6 et son pKa vaut 5.69.
3. Le degré de dissociation a de cet acide est égal à 0.63 %.
4. La concentration des ions hydronium est égale
à 3.16.10-4 mol-1.
La concentration des ions hydroxyde est égale
à 3.16.10-11 mol.L-1.
La concentration des ions A- est égale
à 3.16.10-4 mol.L-1.
La concentration de HA non dissocié est égale
à 4.97.10-2 mol.L-1.
Exercice II.4.
1. La concentration des ions hydronium est égale
à 1.41.10-11 mol.L-1.
La concentration des ions hydroxyde est égale
à 7.08.10-4 mol.L-1.
La concentration des ions ammonium est égale à
7.08.10-4 mol.L-1.
La concentration en ammoniac NH3 non protoné
est égale à 2.81.10-2 mol.L-1.
2. La concentration globale en ammoniaque est égale à 2.88.10-2 mol.L-1.
3. Le degré de protonation a de l'ammoniaque est égal à 2.46 %.
4. La concentration globale de l'ammoniaque après
mélange est égale à 1.152.10-2 mol.L-1.
La valeur du pH de la solution est de 10.65.
La concentration des ions hydronium est égale
à 2.21.10-11 mol.L-1.
La concentration des ions hydroxyde est égale
à 4.53.10-4 mol.L-1.
La concentration des ions ammonium est égale à
4.53.10-4 mol.L-1.
La concentration en ammoniac NH3 non protoné
est égale à 1.148.10-2 mol.L-1.
Le degré de protonation a
de
l'ammoniaque est égal à 3.93 %. C'est normal vu que la dilution
augmente que le degré de protonation augmente: voir le diagramme
de prédominance de l'ammoniaque.
Exercice II.5.
1. Le pH vaut 12.70.
2. Le pH de la solution numéro deux est de 12.40 et le pH du mélange est de 12.57.
3. Le pH vaut 12.48.
Exercice II.6.
1. Le pH vaut 1.30.
La concentration des ions hydronium vaut 5.01.10-2
mol.L-1.
La concentration des ions chlorure vaut 5.01.10-2
mol.L-1.
La concentration des ions hydroxyde est égale
à 2.10-13 mol.L-1.
2. 0.2 g de NaOH équivalent à 5.10-3
mol
de NaOH.
Dans 100 mL de la solution précédente
d'acide chlorhydrique il y a 5.10-3 mol d'ions hydronium et
autant d'ions chlorure.
La soude neutralise exactement l'acide chlorhydrique.
La concentration après réaction des ions
hydronium sera égale à celle des ions hydroxyde donc 10-7
mol.L-1. Le pH vaudra 7.
La concentration des ions spectateurs, le sodium et les
ions chlorures sera égale à 0.05 mol.L-1.
Exercice II.7.
1. Le pH de la solution aqueuse d'acide éthanoïque
vaut 3.03.
La concentration des ions hydronium vaut 9.43.10-4
mol.L-1.
La concentration des ions hydroxyde vaut 1.061.10-11
mol.L-1.
La concentration des ions éthanoate vaut 9.43.10-4
mol.L-1.
La concentration de l'acide éthanoïque moléculaire
non dissocié vaut 4.91.10-2 mol.L-1.
2. 0.2 g de NaOH en cristaux représentent 5.10-3
mol de NaOH.
Dans 100 mL de solution d'acide éthanoïque
précédente il y a 5.10-3 mol d'acide, sous forme
moléculaire ou dissociée.
Après réaction il se sera formé
5.10-3 mol d'éthanoate de sodium. La concentration de
ce sel sera de 5.10-2 mol.L-1.
Le pH de la solution sera égal à 8.72.
On est dans le cas où l'on a un sel d'acide faible
et de base forte, donc qui adopte un comportement de monobase faible de
pKb égal à 9.25 à 25°C.
Exercice II.8.
1. Le pH de la solution d'acide chlorhydrique vaut 3.
Le pH de la solution d'acide éthanoïque vaut
3.38.
2. Le pH après mélange vaut 3.13.
Il faut résoudre l'équation d'électroneutralité
suivante:
Exercice II.9.
1. Le pH de la solution aqueuse d'hydroxyde de sodium
vaut 11.
Le pH de la solution d'ammoniaque vaut 10.63.
2. Après mélange il faudra résoudre l'équation d'électroneutralité suivante:
Exercice II.10.
1. Dans 1 mL d'acide chlorhydrique concentré il
y a 0,32.1,16 g de HCl. Soit 1.017.10-2 mol de HCl.
Si on étend la solution à 1L la concentration
de l'acide chlorhydrique sera égale à 1.017.10-2
mol.L-1.
Le pH sera égal à 1.99.
2. La concentration de l'acide chlorhydrique après
mélange sera égale à 0.020 mol.L-1.
Le pH sera égal à 1.70.
Exercice II.11.
1. Dans 1 mL d'acide sulfurique de densité 1.84
et à 98% en masse en acide sulfurique (teneur de 98%) il y a 0,98.1,84
g d'acide. Soit 1,80 g. Soit, vu que la masse molaire de l'acide sulfurique
est égale à 98 g.mol-1, 1,84.10-2 mol
d'acide sulfurique.
Quand on manipule l'acide sulfurique il faut toujours
verser l'acide sulfurique concentré sur l'eau. En effet c'est au
premier abord une question de densité. L'acide, plus lourd, va au
fond.
Ensuite le sencond point est que la dissolution de l'acide
sulfurique dans l'eau est très exothermique. Si l'on versait l'eau
dessus l'acide on risquerait, vu que l'eau est moins dense que l'acide,
des projections. C'est pourquoi, de toute façon, le port de lunettes
s'impose lorsqu'on prépare des solutions diluées de cet acide
à partir de solutions très concentrées.
On ne doit surtout pas chauffer, mais au contraire refroidir
la solution lorsqu'on fait la dilution. On utilise de l'eau mélangée
à de la glace pilée afin d'évacuer la chaleur dégagée
par la réaction.
Mode opératoire:
Dans un erlenmeyer mettre environ 100 mL d'eau. Plonger
l'erlenmeyer dans un bain d'eau glacée. Rajouter alors, après
avoir chaussé des lunettes de protection, 1 mL d'acide sulfurique
concentré. Agiter. Lorsque la solution est bien refroidie la verser
dans une fiole de 1 L.
Compléter avec de l'eau distillée jusqu'au
trait de jauge et puis boucher, agiter correctement avant utilisation.
Nota: on ne doit jamais avoir la température de
la solution contenue dans de la verrerie de précision qui dépasse
les 20 °C. Si la fiole jaugée était portée à
50 ou 60°C, elle risquerait de perdre sa précision quant à
son volume, garantiseulement à 20 °C.
2. La concentration de la solution d'acide sulfurique sera égale à 1.84.10-2 mol.L-1.
3. Si l'acide est considéré comme un diacide
fort, totalement dissocié le pH de la solution sera égal
à 1.43.
Si l'acide est considéré comme étant
seulement fort pour sa première acidité alors il faut remarquer
que la première acidité libère 1.84.10-2
mol d'ions hydronium par litre de solution.
Lorsqu'intervient la seconde acidité on a l'équilibre
suivant qui intervient:
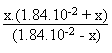
Exercice II.12.
1. La masse molaire de l'acide oxalique cristallisé
dihydraté est égale à 126 g.mol-1.
La concentration de l'acide mis en solution est égale
à 4.76.10-2 mol.L-1.
2. Vu que les pKa respectifs de l'acide oxalique sont
1.2 et 4.3 à 25°C l'acide oxalique se comporte a priori comme
un monoacide faible de pKa égal à pKa1, soit 1.2.
Dans ce cas le pH sera égal à 1.50.
Si l'on veut faire intervenir la deuxième acidité
il faut alors résoudre l'équation du second degré
suivante:
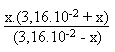
Exercice II.13.
1. La masse molaire du carbonate de sodium est égale à 106 g.mol-1. la concentration de la solution sera de 5.66.10-2 mol.L-1.
2. Le carbonate de sodium se comporte a priori comme une
monobase faible de pKb égal à pKb2, soit 3.70.
Le pH de la solution sera égal à 11.53.
La seconde fonction basique, caractérisée
par un pKb égal à 7.60 est négligeable devant la première.
Chapitre III. Les sels et les hydrogénosels.
Exercice III.1.
1. 3.9 g de chlorure de sodium équivalent à
un nombre de moles égal à 6.67.10-2.
Il faut donc mélanger dans les proportions stoechiométriques
l'acide chlorhydrique et l'hydroxyde de sodium.
La réaction est bien évidemment la suivante:
Pour les cristaux de soude il faut peser une masse équivalant
à la masse de 6.67.10-2 mol de soude, soit 2.668 g de
soude. Il faudra ensuite dissoudre dans un bain d'eau glacée (la
dissolution des cristaux de soude est très exothermique, donc dégage
beaucoup de chaleur) cette masse puis étendre par exemple à
200 mL. La concentration sera alors égale à 0.334 mol.L-1.
On mélangera dans un bain d'eau glacée
les deux solutions et l'on obtiendra après évaporation de
l'eau la masse de sel désirée.
Bien entendu ce sont bien ici des volumes tout à fait "académiques". Il est extrêmement difficile de prélever 6.56 mL de solution acide. Il vaut mieux dans la pratique pipeter par exemple 10 mL de solution et calculer, en fonction de ce volume d'acide prélevé, la quantité de cristaux de soude à peser. C'est nettement plus aisé. On aura alors après évaporation de l'eau une masse de crisatux qui sera supérieure aux 3.9 g requis mais qui vous en empêche, vous pouvez retirer de cette masse la quantité nécessaire afin de vous retrouver avec 3.9 g de chlorure de sodium. Ni vu ni connu et surtout au diable l'académisme. Il faut penser et faire concret en chimie sinon on n'avance pas.
Exercice III.2.
1. Il faudra mélanger deux solutions: l'une d'acide
sulfurique et l'autre d'hydroxyde de potassium, dans les proportions stoechiométriques,
afin d'obtenir le sulfate de dipotassium, alias sulfate de potassium.
L'équation chimique de la salification sera alors:
Exercice III.3.
1. L'équation chimique de la salification de l'acide bromhydrique par l'hydroxyde de potassium est la suivante:
2. Le sel obtenu s'appelle le bromure de potassium, de formule brute KBr.
3. On pourra obtenir après évaporation de l'eau résiduelle 0.01 mol de bromure de potassium. Vu que la masse molaire du bromure de potassium est de 119 g.mol-1, on pourra obtenir une masse de cristaux égale à 1.19 g après évaporation de l'eau.
4. Vu que le bromure de potassium est un sel d'acide fort et de base forte le pH de la solution avant évaporation de l'eau est égal à 7 à 25°C.
Exercice III.4.
1. L'équation de salification de la solution aqueuse d'ammoniaque par l'acide chlorhydrique est la suivante:
2. Le sel obtenu est bien évidemment le chlorure d'ammonium. Sa masse molaire M est égale à 53.5 g.mol-1. On en aura fabriqué ici 6.25.10-3 mol.
3. La masse de chlorure d'ammonium qu'on peut obtenir après évaporation de l'eau résiduelle est égale à 0.334 g.
4. Si l'on avait mesuré le pH de la solution avant évaporation de l'eau, étant donné que la concentration du chlorure d'ammonium était égale à 1.11.10-2 mol.L-1, on aurait trouvé une valeur égale à 5.60. Le chlorure d'ammonium est un sel de base faible et d'acide fort.
Exercice III.5.
1. L'équation de salification de l'acide méthanoïque par l'hydroxyde de potassium est la suivante:
2. Le sel formé s'appellera méthanoate de
potassium, alias formiate de potassium, le second nom de l'acide méthanoïque
étant acide formique.
La masse molaire M de ce sel sera égale à
84 g.mol-1.
3. On pourra espérer recueillir après évaporation de l'eau résiduelle 2.40.10-2 mol de méthanoate de potassium. La masse en sera 2.016 g.
4. Avant évaporation de l'eau résiduelle
la concentration du sel était égale à 4.80.10-2
mol.L-1.
Comme c'est un sel d'acide faible et de base forte le
pH de la solution sera donc basique, puisque le sel adopte le comportement
d'une monobase faible de pKb égal à 10.20.
Le pH sera égal à 8.24.
Exercice III.6.
1. La réaction de salification partielle de l'acide phosphorique est la suivante:
2. Le sel obtenu est un hydrogénosel.
3. La masse de sel anhydre, ne cristallisant avec aucune molécule d'eau, est égale à 4.20 g.
4. Si l'on avait mesuré le pH de la solution avant évaporation de l'eau on aurait trouvé une valeur égale à 4.68, valeur donnée grâce à la formule du pH des hydrogénosels.
Exercice III.7.
1. L'équation de neutralisation partielle du carbonate de sodium en hydrogénocarbonate de sodium et chlorure de sodium est la suivante:
2. Il se sera formé1.755 g de chlorure de sodium et 2.52 g d'hydrogénocarbonate de sodium. Il ne sera pas aisé de les séparer en l'état de façon chimique.
3. Le pH de la solution avant évaporation de l'eau est égal à 8.35. Le pH est imposé par l'hydrogénosel que constitue l'hydrogénocarbonate de sodium. On a une valeur de pH qui est imposée par la formule des hydrogénosels.
Chapitre IV. Les courbes de dosage.
Exercice IV.1.
1. La formule de calcul du pH de la solution, applicable
de V = 0 à V = 39 mL, avec V exprimé en mL, est la
suivante:
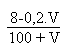
Exercice IV.2.
1. Le pH de la solution , applicable de V = 0 à V = 39 mL, avec V exprimé en mL, est donné par la formule:
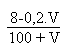
Exercice IV.3.
1. Le nombre de moles initial d'acide chlorhydrique est
égal à 0,08.0,1 soit 8.10-3 mol.
Dans 0,2 g de soude il y a 5.10-3 mol d'ions
hydroxyde.
Si on mélange les deux réactifs il restera
dans 100 mL de solution 3.10-3 mol d'ions hydronium.
Le pH de la solution sera égal à 3.00.
2. On aura:
Exercice IV.4.
1. On devra résoudre l'équation d'électroneutralité suivante:
2. On choisira en abscisses par exemple 1 cm pour 2 mL
de soude versée et en ordonnées 1 cm pour une unité
pH.
3. Le nombre de moles de méthanoate de sodium
HCO2Na obtenu à l'équivalence est égal
à 8.10-3 mol. La masse qu'on peut obtenir, si le sel
cristallise sans emprisonner de molécule d'eau, est égale
à 544 mg.
Exercice IV.5.
1. Avant l'équivalence le pH est imposé
par la soude.
Le pH sera donné par la formule:
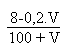
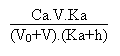
A l'équivalence, lorsque V = 40 mL, on se retrouve
avec une solution aqueuse de méthanoate de sodium de concentration
égale à 0.057 mol.L-1.
Le pH est celui d'un sel d'acide faible et de base forte,
donc celui d'un sel qui a le comportement d'une monobase faible de pKb
égal à 10.2.
Le pH sera donné par la formule:
Exercice IV.6.
1. Le pH initial de la solution d'ammoniaque est donné a priori par la formule:
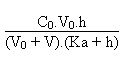
A l'équivalence, lorsque le volume V d'acide chlorhydrique
versé est égal à 40 mL, on sera en présence
d'une solution aqueuse de chlorure d'ammonium de concentration égale
à 0.057 mol.L-1.
Le pH de la solution de ce sel d'acide fort et de base
faible, qui adopte le comportement par conséquent d'un monoacide
faible de pH égal à pKa, sera donné a priori par la
formule:
Au-delà de V = 40 mL le pH de la solution est imposé
par l'acide chlorhydrique en excès.
Le pH de la solution sera donné par la relation:
Exercice IV.7.
1. Avant l'équivalence le pH de la solution est
imposé par la solution d'acide chlorhydrique, acide fort.
On aura alors:
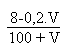
Au-delà de V = 40 mL il faut résoudre l'équation d'électroneutralité suivante:
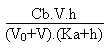
2. Pour tracer la courbe on choisira en abscisses par exemple 1 cm pour 2 mL versés et en ordonnées 1 cm pour une unité pH.
Exercice IV.8.
1. Comme l'acide sulfurique est un diacide dont seule la première acidité est totale , la seconde ayant un pKa de l'orde de 1.9, le pH de la solution en fonction du volume V de soude versée est donné par l'équation de l'électroneutralité suivante:
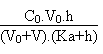
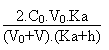
A l'équivalence, soit pour un volume V égal
à 80 mL (l'acide sulfurique est un diacide) on a une solution aqueuse
de sulfate de sodium de concentration égale à 0.044 mol.L-1.
A priori l'anion sulfate réagit avec l'eau pour
régénérer des ions hydrogénosulfate et des
ions hydroxyde selon l'équation:
Au-delà du volume équivalent ce sera la
solution de soude qui imposera son pH.
On aura alors:
3. On pourra recueillir une masse m de sulfate de sodium égale à 1.136 g après avoir évaporé l'eau résiduelle. Il s'est formé 8.10-3 mol de sulfate de sodium.
4. Si l'on considère que l'acide sulfurique est un véritable diacide fort on constate que la courbe donnant le pH en fonction de V est située en-dessous de la courbe réelle. Le pH au point de départ vaut alors 0.80 (du moins en théorie) au lieu de 1.05, valeur calculée en 1.
Exercice IV.9.
1. Etant donné que les deux pKa de l'acide sulfhydrique
ont pour valeurs respectives 7.00 et 13.00 à 25°C les deux acidités
de H2S seront dosées séparément.
On divisera la courbe en trois parties.
Première partie: de V = 0 à V = 40 mL.
De V/Ve = 0 à V/Ve = 1.
Deuxième partie: de V = 40 à V = 80 mL.
De V/Ve = 1 à V/Ve = 2.
Troisième partie: au-delà de V = 80 mL.
Au-delà de V/Ve = 2.
Première partie:
Le pH initial vaut 4.05 étant donné
que H2S se comporte comme un monoacide faible, dans la pratique,
de pKa égal à pKa1, soit 7.
Lorsque V = 40 mL on a une solution aqueuse d' hydrogénosulfure
de sodium NaHS, un hydrogénosel, de concentration égale
à 0.057 mol.L-1. Le pH de la solution est égal
à 10.
Entre les deux valeurs le pH est donné par l'équation
d'électroneutralité suivante:
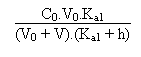
Exemple: que vaut le pH de la solution lorsque V = 13
mL?
En postulant que le pH sera acide on est amené
à résoudre l' équation du second degré suivante:
Deuxième partie: entre V = 40 et V = 80 mL.
Pour V = 80 mL on est en présence d' une solution
aqueuse de sulfure de disodium Na2S de concentration égale
à 0.044 mol.L-1. Il faut résoudre l'équation
du second degré obtenue à partir de:
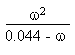
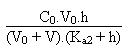
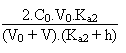
Troisième partie: au-delà de V = 80 mL.
La soude impose son pH au milieu.
Le pH sera donné par la formule:
3. Il s'est formé 8.10-3 mol de sulfure de disodium Na2S. La masse de sel susceptible d'être obtenue après évaporation de l'eau est égale à 624 mg.
4. Le sulfure de dihydrogène sent... les oeufs pourris....
Retour au plan du cours sur les pH des solutions aqueuses.
Suite des corrigés des exercices sur les pH des solutions aqueuses.