Retour au plan du cours sur la classification périodique.
C' est, de loin, le bloc le plus complexe, de la classification périodique.
C' est un bloc de métaux.
Nous avons vu que pour les blocs s et p la structure électronique
des atomes des éléments de ces blocs respectait toujours
la règle mnémotechnique de KLECHKOWSKY.
Ce sont donc des blocs homogènes.
Le bloc d est beaucoup moins ordonné, si l' on peut dire.
Il rassemble les colonnes 3, 4, 5, 6, 7, 8, 9, 10, 11 et 12 du tableau périodique.
Nous avons vu, lors de la construction de la classification, que la première ligne du bloc d, la période "3d" admettait deux exceptions à la règle mnémotechnique de KLECHKOWSKY, le chrome ( Z = 24) et le cuivre ( Z = 29).
Lorsqu' on regarde la classification colonne par colonne l' hétérogénéité des résultats est plus grande.
Je ne donnerai ici que des résultats et dirai s'
il y a lieu de comprendre l' hétérogénéité
de ces derniers.
A défaut, les résultats s' imposeront d'
eux mêmes et les explications, si explications il y a, à l'
heure actuelle, suivront...un peu plus tard, au gré du développement
de la compréhension par la chimie du monde réel.
N' oublions jamais que la chimie est une science expérimentale et que sa théorie ne se nourrit que de la confrontation de celle ci avec l' expérience.
Les colonnes les moins compliquées du bloc d sont les colonnes 7 et 12.
Colonne 7.
Les trois éléments qui la composent, à savoir le manganèse (Z = 25), le technétium (Z = 43) et le rhénium (Z = 75), obéissent tous à la règle de KLECHKOWSKY pour ce qui concerne les atomes de leurs éléments.
On rencontrera facilement le degré d' oxydation
+II pour le manganèse.
Ce seront les électrons 4s qui partiront avant
les électrons 3d. Le cation Mn ( II ) aura la structure électronique
suivante: [ Ar ] 3d5.
C' est ce qu' on sera censé retenir pour cette
colonne.
Pour ce qui est du technétium et du rhénium,
ce sera le degré d' oxydation + VII qui sera le degré d'
oxydation de ces éléments pris dans des ions plus ou moins
complexes. Ce degré d' oxydation aussi élevé sera
vraisemblablement un degré d' oxydation formel, un peu comme le
degré d' oxydation + VI du chrome dans l' anion dichromate Cr2O72-.
Il est en effet difficile d' imaginer des cations Tc7+ ou Re7+.
| Colonne 7 | Nom | Structure électronique |
| 25Mn | Manganèse | [ Ar ] 4s2 3d5 |
| 43Tc | Technécium | [ Kr ] 5s2 4d5 |
| 75Re | Rhénium | [ Xe ] 6s2 5d5 4f14 |
Colonne 12.
Les trois éléments qui la composent, et
qui sont, respectivement le zinc ( Z = 30 ), le cadmium ( Z = 48 ), et
le mercure ( Z = 80 ), obéissent à la règle de KLECHKOWSKY.
| Colonne 12 | Nom | Structure électronique |
| 30Zn | Zinc | [ Ar ] 4s2 3d10 |
| 48Cd | Cadmium | [ Kr ] 5s2 4d10 |
| 80Hg | Mercure | [ Xe ] 6s2 5d10
4f 14 |
On rencontrera aisément, pour ces trois métaux
le degré d' oxydation + II.
En perdant les deux électrons qui se trouvent
respectivement dans les sous-couches externes 4s, ou 5s, ou 6s, les atomes
de ces éléments chimiques deviennent des "pseudo gaz rares",
puisqu' ils ont acquis la configuration électronique du gaz rare
qui les précède avec, en plus, la sous-couche ( n - 1 )d
qui est complètement remplie.
On remarquera encore que ce sont bien les électrons
ns qui partent avant les électrons
( n - 1 )d, erreur souvent commise lors des examens.
| Cations divalents issus des éléments de la colonne 12. | Nom | Structure électronique |
| 30Zn2+ | Cation zinc
( II ) |
[ Ar ] 3d10 |
| 48Cd2+ | Cation cadmium
( II ) |
[ Kr ] 4d10 |
| 80Hg2+ | Cation mercure
( II ) |
[ Xe ] 5d10 |
C' est ce qu' il sera suffisant de retenir.
Pour le mercure on peut signaler, qu' outre le degré
d' oxydation + II, dans le cation Hg2+, que l' on vient d' écrire,
il existe le degré d' oxydation + I.
Cet ion mercure ( I ), Hg ( I ), qui a la structure
électronique suivante: [ Xe ] 6s1 5d10 subit
la tendance à la dimérisation en cation dimercure ( II ),
Hg22+, dont le degré d' oxydation de l' élément
mercure est toujours + I.
Il se crée une liaison de covalence entre les deux cations isolés Hg+ et c' est ce qui décrit le mieux la formation d' un tel dimère.
Le cation dimercure ( II ) Hg22+ entre dans la composition de l' électrode au calomel saturée, c' est à dire dans la composition de l' électrode combinée "verre-calomel" servant à la détermination des pH des solutions aqueuses, le calomel n' étant rien d' autre que le dichlorure de dimercure (II), anciennement appelé chlorure mercureux, de formule chimique Hg2Cl2.
On ne connaît pas un tel phénomène avec le cadmium et le zinc.
La complexité du bloc d ne fait que commencer.
La colonne 11, immédiatement contiguë à
la précédente est homogène dans les exceptions à
la règle mnémotechnique de KLECHKOWSKY.
Cette colonne est composée respectivement des
éléments cuivre ( Z = 29 ), argent ( Z = 47 ) et or ( Z =
79 ).
| Colonne 11 | Nom | Structure électronique. |
| 29Cu | Cuivre | [ Ar ] 4s1 3d10 |
| 47Ag | Argent | [ Kr ] 5s1 4d10 |
| 79Au | Or | [ Xe ] 6s1 5d10 4f14 |
On connaît pour les atomes de ces éléments
des cations monovalents, de degré d' oxydation +I.
| Cations monovalents des éléments de la colonne 11 | Nom | Structure électronique |
| 29Cu+ | Cation
Cuivre ( I ) |
[ Ar ] 3d10 |
| 47Ag+ | Cation
Argent ( I ) |
[ Kr ] 4d10 |
| 79Au+ | Cation
Or ( I ) |
[ Xe ] 5d10 4f14 |
C' est le cation Ag ( I ) qui est le plus connu. Sa stabilité est très grande.
Pour l' or et le cuivre on connaît également
d' autres degrés d' oxydation stables.
Pour le cuivre il s' agit du cation cuivre ( II ),
Cu ( II ), de structure électronique [ Ar ] 3d9, beaucoup
plus stable en solution aqueuse que le cation Cu ( I ), et pour l'
or, le cation Au ( III ), de structure électronique [ Xe ] 5d8
4f14.
Tout cela n' était pas directement accessible au vu de la classification périodique, ce qui illustre, une fois de plus, la complexité du réel.
La colonne 6 est sans doute la plus hétérogène.
| Colonne 6 | Nom | Structure électronique |
| 24Cr | Chrome | [ Ar ] 4s1 3d5 |
| 42Mo | Molybdène | [ Kr ] 5s1 5d5 |
| 74W | Tungstène
(anciennement wolfram) |
[ Xe ] 6s2 5d4 4f14 |
Afin de montrer qu' il est très difficile de généraliser
en chimie je trouve que cette colonne 16 en est un bel exemple.
En effet, on a vu que le chrome n' obéissait pas
à la règle mnémotechnique de KLECHKOWSKY parce que
la stabilité des orbitales 3d était plus grande lorsque ces
dernières étaient à moitié remplies, voire
totalement remplies.
Cela se vérifie por le chrome et le molybdène
mais pas pour le tungstène, qui garde sa configuration électronique
en 6s2 5d4.
Que conclure de cette brève revue de quelques colonnes du bloc d?
Les orbitales ( n - 1 )d sont complexes. Du fait qu' elles soient incomplètement remplies et d' énergie voisine des orbitales ns, il existe de nombreuses possibilités de réarrangements électroniques qui donnent naissance à de très nombreux degrés d' oxydation stables pour les atomes de ces éléments.
L' étude approfondie des éléments du bloc d se fera au cours du second cycle de chimie, lorsqu' on étudiera la chimie de coordination. Il existe en effet de très nombreux composés chimiques qui peuvent réagir avec des atomes ou des ions issus des métaux du bloc d: on obtiendra des complexes aux applications très diverses, notamment dans le domaine de la synthèse organique ou de la catalyse.
Retour au plan du cours sur la classification périodique.
Retour au plan du cours sur la classification périodique.
Après l' élément barym, Ba, Z = 56, l' élément 57, qui est le lanthane, La, devrait avoir, si l' on suit la règle mnémotechnique de KLECHKOWSKY, la structure électronique suivante:
Or, le lanthane est une exception à cette règle
mnémotechnique.
Sa structure réelle est:
A ce titre il est le premier élément du bloc 5d, c' est à dire l' élément qui est dans la période n = 6 et dans la colonne 3 du tableau périodique.
L' élément suivant, le cérium, Ce, Z = 58, devrait avoir pour structure électronique, d' après la règle mnémotechnique de KLECHKOWSKY:
C' est d' ailleurs cette structure qui est réellement observée.
A partir du cérium, on commence à trouver des éléments qui contiennent des électrons dans la sous-couche 4f.
Comme cette sous-couche peut contenir 14 électrons
au maximum on aura en tout 14 éléments à placer.
Pour bien faire il aurait fallu imaginer une classification
périodique avec , non pas 18 colonnes, mais 32 colonnes.
Pour des raisons évidentes de commodité on a préféré désolidariser ce bloc de 14 éléments (pour la sous-couche 4f seulement) dans ce que l' on va appeler le bloc f.
C' est pour cette raison qu' on rencontre le bloc f placé en dessous des trois blocs accolés s, p et d.
Les quatrorze éléments qui suivent le lanthane
sont appelés "lanthanides". Ils font partie de ce qu' on appelle
en chimie inorganique des "terres rares".
Ces éléments sont, dans l' ordre:
| Elément chimique | Nom | Structure électronique |
| 58Ce | Cérium | [ Xe ] 6s2 4f2 |
| 59Pr | Praséodyme | [ Xe ] 6s2 4f3 |
| 60Nd | Néodyme | [ Xe ] 6s2 4f4 |
| 61Pm | Prométhéum | [ Xe ] 6s2 4f5 |
| 62Sm | Samarium | [ Xe ] 6s2 4f6 |
| 63Eu | Europium | [ Xe ] 6s2 4f7 |
| 64Gd | Gadolinium | [ Xe ] 6s2 5d1 4f7 |
| 65Tb | Terbium | [ Xe ] 6s2 4f9 |
| 66Dy | Dysprosium | [ Xe ] 6s2 4f10 |
| 67Ho | Holmium | [ Xe ] 6s2 4f11 |
| 68Er | Erbium |
[ Xe ] 6s2 4f12
|
| 69Tm | Thullium | [ Xe ] 6s2 4f13 |
| 70Yb | Ytterbium | [ Xe ] 6s2 4f14 |
| 71Lu | Lutécium | [ Xe ] 6s2 4f14 5d1 |
Les terres rares sont utilisées dans de nombreuses
applications de physique et de chimie.
On les rencontre dans les écrans de télévision
couleur, afin de donner l' effet de couleur.
On les rencontre aussi dans... les pierres de briquets....
Sans oublier les sels d' europium notamment, qu' on utilise
en chimie analytique, en résonance magnétique nucléaire,
la RMN, afin d' élucider la structure chimique de molécules
organiques.
Après le radium, Ra, Z = 88, de structure électronique égale à:
Or, l' actinium est aussi une exception à la règle
de KLECHKOWSKY, tout comme le lanthane qui suivait le baryum, l' élément
de la colonne des alcalino-terreux juste au dessus du radium.
Sa structure électronique réelle est:
C' est donc le premier élément du bloc 6d, tout comme le lanthane était le premier élément du bloc 5d.
A la suite de l' actinium on rencontre l' élément
de numéro atomique Z = 90, le thorium, symbole Th.
La structure électronique des atomes de l' élément
thorium, pris dans leur état fondamental, est:
Les orbitales 6d et 5f sont très proches énergétiquement.
On considère qu' à partir du thorium, donc
à partir de Z = 90, on commence la famille des "actinides", c' est
à dire la famille des quatorze éléments qui suivent
l' actinium.
On aura alors:
| Elément chimique | Nom | Structure électronique |
| 90Th | Thorium | [ Rn ] 7s2 6d2 |
| 91Pa | Proctatinium | [ Rn ] 7s2 6d1 5f2 |
| 92U | Uranium | [ Rn ] 7s2 6d1 5f3 |
| 93Np | Neptunium | [ Rn ] 7s2 5f5 |
| 94Pu | Plutonium | [ Rn ] 7s2 5f6 |
| 95Am | Américium | [ Rn ] 7s2 5f7 |
| 96Cm | Curium | [ Rn ] 7s2 6d1 5f7 |
| 97Bk | Berkélium | [ Rn ] 7s2 5f9 |
| 98Cf | Californium | [ Rn ] 7s2 5f10 |
| 99Es | Einsteinium | [ Rn ] 7s2 5f11 |
| 100Fm | Fermium | [ Rn ] 7s2 5f12 |
| 101Md | Mendelevium | [ Rn ] 7s2 5f13 |
| 102No | Nobélium | [ Rn ] 7s2 5f14 |
| 103Lw | Lawrencium | [ Rn ] 7s2 6d1 5f14 |
Au-delà de l' uranium, le dernier élément
naturel, on aborde ce que l' on appelle les "transuraniens", c' est à
dire des éléments artificiels, élaborés à
partir de 1945 et des travaux sur le noyau atomique, qui ont conduit notamment
à l' élaboration de la bombe atomique.
Le plus célèbre d' entre eux est le plutonium,
de symbole Pu.
Au-delà de l' élément 103, le lawrencium,
Lw, on repart sur le bloc d, plus exactement le bloc 6d.
Ce sont là aussi des éléments artificiels,
dont les noms avaient donné, lors de la rivalité Etats-Unis-
URSS, à des "conflits" entre les centres de recherches américain
( Berkeley) et soviétique (Dubna).
Aujourd' hui, après avoir cherché à
systématiser leur nom, comme Unq, l' élément 104 par
exemple, le " unnihilquadium" (un = 1; nihil = 0; quad = 4; d' où
"104") on les désigne comme suit, sans que cela ne provoque
plus aucun "conflit":
| Elément chimique | Nom | Structure électronique |
| 104Ru | Rutherfordium
(anc. Kourtchatovium) |
[ Rn ] 7s2 6d2 5f14 |
| 105Db | Doubnium | [ Rn ] 7s2 6d3 5f14 |
| 106Bh | Bohrium | [ Rn ] 7s2 6d5 5f14 |
| 107Hs | Hassium | [ Rn ] 7s2 6d6 5f14 |
| 108Mt | Meitnerium | [ Rn ] 7s2 6d7 5f14 |
Au-delà les éléments ne sont pas
caractérisés par leur structure électronique.
Souvent ce sont des éléments instables,
qui ont donc une durée de vie très réduite et, pour
certains d' entre eux, on n' en possède que... quelques atomes....
On a synthétisé, à l' heure actuelle,
des noyaux lourds allant jusqu' à Z = 118.
Retour au plan du cours sur la classification périodique.
III.6. Evolution des propriétés.
Retour au plan du cours sur la classification périodique.
III.6.1. Evolution des rayons atomiques.
Retour au plan du cours sur la classification périodique.
On remarque qu' il y a:
Décroissance du rayon lorsqu' on se déplace dans une période donnée dans le sens des numéros atomiques Z croissants.
Ainsi, dans la période M, de nombre quantique principal n = 3, le rayon de l' atome de sodium ( Z = 11) est plus grand que celui de l' atome de chlore (Z = 17).
Lorsqu' on change de période on constate une brusque augmentation du rayon atomique entre l' atome d' halogène de la période n et l' atome de métal alcalin de la période n +1.
Lorsqu' on descend dans une colonne le rayon atomique augmente.
Comment essayer d' expliquer cela?
On introduit alors le modèle de SLATER. On précise bien que ce n' est qu' un modèle.
SLATER classe les orbitales atomiques par "paquets d' orbitales" ayant des énergies voisines.
Ainsi, on se retrouve avec les paquets suivants:
| Paquets d' orbitales atomiques ayant des énergies voisines |
| 1s |
| 2s 2p |
| 3s 3p |
| 3d |
| 4s 4p |
| 4d |
| 4f |
| 5s 5 p |
SLATER introduit alors ce qu' on appellera la "constante d' écran", qu' on notera s.
SLATER considère que dans un atome polyélectronique les électrons de la couche périphérique, celle qui crée en quelque sorte le rayon, donc le volume de l' atome, ne "voient pas" les Z protons du noyau atomique mais juste une fraction, étant donné que les électrons des couches internes "masquent" une partie du noyau atomique à ces électrons périphériques.
A partir de ce postulat SLATER évalue, c' est à dire chiffre, l' effet d' écran induit par ces électrons internes.
La constante d' écran s sera égale alors à la somme des effets d' écran produits par tous les électrons situés entre le noyau et la couche périphérique.
A partir de là SLATER calcule la charge efficace, notée Z*, perçue par les électrons périphériques avec:
Pour un électron situé sur une orbitale
1s l' effet d' écran produit par l' autre électron en 1s
est égal à 0.30.
Pour un électron situé dans une orbitale
ns ou np, avec n supérieur à 1, l' effet d' écran
subi de la part de chacun des autres électrons de son groupe
est égal à 0.35.
L' effet d' écran subi par ce même électron
de la part des électrons de niveau immédiatement inférieur
est égal à 0.85 par électron.
L' effet d' écran subi par cet électron
de la part des niveaux inférieurs au niveau immédiatement
inférieur est égal à 1.00 par électron.
D' autre part, les électrons situés sur
des niveaux énergétiques supérieurs au niveau considéré
ne produisent aucun effet d' écran sur l' électron considéré
ici.
Un exemple: quelle est la charge effective perçue par un électron périphérique de l' atome de soufre? On précise que le numéro atomique du soufre est Z = 16.
D' après SLATER on classe les orbitales de l' atome
de soufre comme suit:
Premier paquet: orbitale 1s: 2 électrons.
Deuxième paquet: orbitales 2s et 2p: 8 électrons.
C' est à dire 2 + 6.
Troisième paquet: orbitales 3s et 3p: 6 électrons.
C' est à dire 2 + 4.
Si l' on considère l' effet d' écran constitué
par les 15 électrons de l' atome de soufre sur l' un des électrons
périphériques on arrive à:
1. Effet d' écran subi par un électron
périphérique de la part de ses 5 autres congénères:
5. 0.35 = 1.75.
Effet d' écran subi par un des électrons
périphériques de la part des électrons situés
dans le paquet énergétique immédiatemment inférieur:
8. 0.85 = 6.80.
Effet d' écran subi par l' un des électrons
périphériques de la part des électrons situés
dans le paquet 1s: 2. 1.00 = 2.00.
On additionne les contributions:
1.75 + 6.80 + 2.00 = 10.55.
La valeur efficace de Z vaut alors: 16 - 10.55 = 5.45.
A partir de là SLATER définit le rayon d' une orbitale par:
A partir de là, on pourra parler d' orbitale de valence comme étant l' orbitale, ou le paquet d' orbitales, correspondant à la couche externe d' un atome polyélectronique donné.
SLATER définira alors le rayon atomique d' un atome polyélectronique par: la valeur du rayon des orbitales de valence de l' atome.
Dans le cas de l' atome de soufre le rayon atomique sera
calculé à partir:
1. Des orbitales de valence, c' est à dire le
paquet 3s et 3p, caractérisé par le nombre quantique n égal
à 3.
2. Du rayon de BOHR: 53 pm.
3. De la charge efficace du noyau de l' atome de soufre,
à savoir 5.45.
On trouve alors la valeur 87 pm pour le "rayon atomique" de l' atome de l' élément soufre, pris, bien sûr, dans son état fondamental .
Retour au plan du cours sur la classification périodique.
III.6.2. Energie de première ionisation des atomes.
Retour au plan du cours sur la classification périodique.
Cette énergie correspond à l' énergie qu' il faut fournir à un atome, donc énergie comptée positivement, pour lui arracher un électron.
Soit le processus:
A ![]() A+
+ 1 e.
A+
+ 1 e.
L' évolution est la même pour les éléments alcalino-terreux.
Il est simplement plus facile d' arracher un électron célibataire à un atome d' un élément alcalin que d' arracher un électron à un atome d' élément alcalino-terreux, contigu exactement du premier.
Ainsi il faudra par exemple fournir 9.3 eV pour obtenir Be+ à partir du premier élément chimique alcalino-terreux Be (Z = 4), alors qu' il ne faudra que 5.4 eV pour obtenir Li+ à partir de Li (Z = 3), le premier élément chimique de la famille des alcalins.
Les deux électrons ns sont appariés dans l' atome de l' élément alcalino-terreux et il est "évident" au sens intuitif qu' il est plus difficile de désolidariser un "couple" qu' un électron tout seul.
Il sera en revanche difficile, c' est à dire coûteux en énergie, d' ioniser les atomes des éléments chimiques de la colonne des halogènes ou, a plus forte raison, de celle des gaz rares.
Les mêmes remarques concernant l' évolution de l' énergie de première ionisation sont valables pour les atomes d' halogènes et des gaz rares comme pour ce qui a été dit pour les alcalins et les alcalino- terreux.
On retrouve alors un diagramme" Energie de première ionisation en fonction de Z" qui est en dents de scie.
SLATER a proposé un modèle pour calculer
théoriquement cette énergie de première ionisation.
Ce calcul marche assez bien pour certains atomes mais
se complique sacrément pour d' autres.
Je le donne à titre d 'illustration.
SLATER définit l' énergie électronique d' un électron d' un atome polyélectronique par:
E élémentaire d' un électron
= 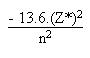
SLATER appelle alors énergie électronique totale d' un atome polyélectronique la somme:
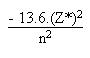
Application numérique:
Quelle est l' énergie de première ionisation de l' atome d' azote ( Z = 7) calculable par ce modèle et comparer cette valeur calculée à la valeur expérimentale, à savoir 14.5 eV?
Le processus est le suivant:
La structure électronique de l' atome d' azote
N est: 1s2 2s2 2p3.
La structure électronique du cation N+
est: 1s2 2s2 2p2.
Les paquets énergétiques d' orbitales sont, d' après SLATER : "1s" d' une part, et "2s 2p" d' autre part.
Pour un électron 1s la charge efficace du noyau
atomique de l' azote est: 7 - 0.30, soit 6.70.
Pour un électron 2s ou 2p la charge efficace est
:
1. Dans l' atome d' azote N: 7 - ( 4.0.35 + 2.0.85)
= 7 - 3.10 = 3.90.
2. Dans le cation N+: 7 - ( 3.0.35 + 2.0.85)
= 7 - 2.75 = 4.25.
Ainsi, l' énergie électronique totale de
l' atome d' azote N est égale à:
E ( N ) = - 13.6. [ 2.(6.70/1)2 + 5.(3.90/2)2]
, soit - 1479.60 eV.
Pour le cation N+ ce sera alors:
E ( N+ ) = -13.6. [ 2.(6.70/1)2
+ 4.(4.25/2)2], soit -1466.66 eV.
Lors du processus d' ionisation l' énergie mise en jeu est la suivante:
Pour le carbone, dans un processus analogue, on trouve 11.46 eV (valeur théorique) et 11.3 eV (valeur expérimentale). Le pourcentage d' erreur est de 1.4% seulement.
Il ne faut surtout pas perdre de vue que ce n' est qu' un modèle, avec TOUTES LES LIMITES que cela comporte.
Retour au plan du cours sur la classification périodique.
III.6.3. Affinité électronique.
Retour au plan du cours sur la classification périodique.
L' affinité électronique est l' énergie qui est mise en oeuvre pour fixer un électron sur un atome.
Soit le processus:
Les alcalino-terreux n' ont pas d' affinité électronique.
On ne connaît pas d' anion Mg- par exemple.
Idem pour les gaz rares.
C' est une donnée expérimentale qui fournit
des renseignements beaucoup moins précis que l' énergie de
première ionisation.
L' affinité électronique a tendance à
augmenter (attention, mettre un bémol) lorsqu' on se déplace
sur une période.
Le long d' une colonne c' est moins évident.
III.6.4. Echelle d' électronégativité de PAULING.
Retour au plan du cours sur la classification périodique.
Il y a eu, avant l' échelle de PAULING, d' autres échelles d' électronégativité qui, toutes, ont voulu donner une idée de classement entre atomes qui avaient tendance à attirer des électrons de liaison vers eux ou, au contraire, avaient tendance à les repousser.
D' après MULLIKEN l' électronégativité E.N. d' un atome d' un élément chimique entrant dans une liaison chimique est donnée par définition par:
Comme on ne connaît pas l' affinité électronique de tous les éléments chimiques cette échelle a connu moins de succès que celle de PAULING, beaucoup plus étendue.
Linus PAULING ( Américain, Prix NOBEL de Chimie
en 1954, mort en 1994) avait constaté que l' énergie de dissociation
expérimentale des halogénures d' hydrogène était
supérieure à celle que l' on pouvait calculer à partir
des énergies expérimentales de dissociation des molécules
de dihydrogène H2 et de dihalogène X2.
A partir de là il a construit son échelle,
du moins en partie.
Il a fixé à 4.00 la valeur de l' électronégativité de l' élément le plus électronégatif de la classification périodique, le fluor.
Exemple de calcul:
Calcul de l' électronégativité cCl
des atomes de l' élément chlore.
Données:
Energie de dissociation expérimentale de
la molécule de dihydrogène H2: 430.5 kJ.mol-1.
Energie de dissociation expérimentale de la molécule
de dichlore Cl2: 243 kJ.mol-1.
Energie de dissociation expérimentale de la molécule
de chlorure d' hydrogène HCl: 426 kJ.mol-1.
Electronégativité
c H des atomes de l' élément
hydrogène dans la classification des électronégativités
de L. PAULING: 2.20.
Valeur du nombre d' AVOGADRO: 6.02.1023.
1 eV = 1.6.10-19 J.
Calcul de l' énergie de dissociation théorique de la molécule de chlorure d' hydrogène HCl:
PAULING pose alors, comme définition de cette
énergie de dissociation théorique, qu' elle st égale
à la moyenne géométrique des énergies de dissociation
expérimentales des molécules de dihydrogène
et de dichlore.
Soit:
Il faut juste, au niveau des unités, transformer les kJ.mol-1 en eV.molécule-1.
On arrive alors à:
Le terme correcteur 0.014 est celui qui permet de passer
des kJ.mol-1 aux eV.molécule-1
0.014 = (1000/6.02.1023.1.6.10-19)
On trouve alors que l' électronégativité
cCl
est égale à 3.23.
Ainsi dans la molécule de chlorure d' hydrogène
HCl on aura bien, comme on le sait depuis longtemps, les électrons
de la liaison de covalence qui seront davantage attirés par l' atome
de chlore que par l' atome d' hydrogène. La différence d'
électronégativité jouant en faveur du chlore.
D' où la polarisation de la molécule de
chlorure d' hydrogène HCl en d+
et d-.
| d+ | Liaison covalente. | d- |
| H | - | Cl |
De façon très générale:
On constate que dans une colonne l' électronégativité
chute lorsque Z augmente.
On constate que dans une période l' électronégativité
augmente lorsque Z augmente.
A la gauche du tableau périodique on rencontre les éléments les moins électronégatifs: ce sont les métaux. Ils ont tendance surtout à perdre des électrons ou à repousser des électrons lorsqu' ils forment une liaison chimique.
A la droite du tableau périodique on rencontre
les éléments les plus électronégatifs: ce sont
les non métaux.
Ils ont tendance à attirer les électrons
lorsque des atomes de ces éléments sont engagés dans
une liaison chimique.
L' élément le plus électronégatif
du tableau périodique est le fluor F, Z = 9, un halogène.
Son électronégativité dans l' échelle de PAULING
vaut 4.00.
L' élément le moins électronégatif
du tableau périodique est le césium, Z = 55, un métal
alcalin. Son électronégativité dans l' échelle
de PAULING vaut 0.7.
Echelle d' électronégativité de PAULING
pour quelques éléments chimiques.
La colonne 18, celle des gaz rares a été
supprimée, étant donné que ces derniers n' ont pratiquement
aucune affinité chimique pour qui que ce soit.
| . | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| K | H
2.20 |
||||||||||||||||
| L | Li
1.0 |
Be
1.5 |
B
2.0 |
C
2.5 |
N
3.0 |
O
3.5 |
F
4.0 |
||||||||||
| M | Na
0.9 |
Mg
1.2 |
Al
1.5 |
Si
1.8 |
P
2.1 |
S
2.5 |
Cl
3.0 |
||||||||||
| N | K
0.8 |
Ca
1.0 |
Sc
1.3 |
Ti
1.5 |
V
1.7 |
Cr
1.6 |
Mn
1.5 |
Fe
1.7 |
Co
1.7 |
Ni
1.8 |
Cu
1.9 |
Zn
1.5 |
Ga
1.6 |
Ge
1.8 |
As
2.0 |
Se
2.4 |
Br
2.8 |
| O | Rb
0.8 |
Sr
1.0 |
Y
1.2 |
Zr
1.4 |
Nb
1.7 |
Mo
1.6 |
Tc
1.9 |
Ru
2.0 |
Rh
2.1 |
Pd
2.0 |
Ag
1.8 |
Cd
1.5 |
In
1.5 |
Sn
1.8 |
Sb
1.9 |
Te
2.1 |
I
2.5 |
| P | Cs
0.7 |
Ba
0.9 |
La
1.0 |
Hf
1.5 |
Ta
1.5 |
W
1.9 |
Re
2.1 |
Os
2.0 |
Ir
2.1 |
Pt
2.1 |
Au
2.3 |
Hg
1.8 |
Tl
1.7 |
Pb
1.9 |
Bi
1.9 |
Po
2.0 |
At
2.2 |
| Q | Fr
0.7 |
Ra
0.9 |
Ac
1.1 |
La connaissance de l' électronégativité
des éléments chimiques permet également de donner
le nom le plus approprié à des molécules telles que
F2O, qui est un gaz.
Faut-il l' appeler oxyde de difluor ou bien difluorure
d' oxygène, soit, plus simplement, fluorure d' oxygène?
Dans l' échelle de PAULING le fluor est plus électronégatif
que l' oxygène, par conséquent c' est plutôt lui qui
aura tendance à attirer les électrons de covalence. La formule
limite de F2O serait alors O2+ + 2F-.
Comme l' anion F- est appelé fluorure
alors on appellera F2O fluorure d' oxygène (difluorure
d' oxygène pour être encore plus précis) et non pas
oxyde de difluor, lequel supposerait une électronégativité
plus grande pour l' oxygène que pour le fluor.
PAULING généralise ensuite ses résultats
et publie l' allure générale de l' évolution des électronégativités
des éléments chimiques, les gaz rares exceptés.