Retour au plan du cours sur les pH des solutions aqueuses.
La pH métrie est une technique potentiométrique, basée sur la mesure de la différence de potentiel entre deux électrodes: une électrode de référence, l' électrode au calomel, saturée en KCl, et une électrode de mesure, l' électrode de verre.
En revanche, la conductimétrie est une méthode électrique, basée sur la mesure de la variation de la résistance électrique d' un milieu ionique, tel qu' une solution aqueuse d' acide et/ou de base.
La mesure se fait à l' aide d' une sonde, constituée
de deux plaquettes de platine "platiné", de surface en vis-à-vis
S, et espacées d' une longueur l.
Cette sonde est plongée complètement, au
niveau de ses deux plaquettes, dans la solution à étudier.
La résistance R de la solution est alors proportionnelle
à l et inversement proportionnelle à S.
L' homogénéité des formules oblige
alors à introduire une caractéristique intrinsèque
de la solution, la résistivité r de
la solution.
On aura alors:
On utilise souvent, au lieu de la résistance R,
son inverse, la "conductance", notée L, d' unité le "siemens",
de symbole S, lorsque R est exprimée en W.
Le rapport![]() est
désigné par K, constante de cellule. Si l est en m et S en
m2, alors K est en m-1. Il caractérise la
forme intrinsèque de la cellule de mesure.
est
désigné par K, constante de cellule. Si l est en m et S en
m2, alors K est en m-1. Il caractérise la
forme intrinsèque de la cellule de mesure.
La résistivité r de la solution admet aussi un inverse, noté s, qui est appelé "conductivité" , et dont l' unité est le siemens par mètre, noté S.m-1, lorsque r est exprimée en W.m.
On aura alors:
![]() = R =
= R = ![]()
On a ici, sous forme de tableau, les valeurs des conductivités,
exprimées en mS.cm-1, de solutions de chlorure de potassium,
à 0.1 mol.L-1, à diverses températures.
| Température ( ° C ) | Conductivité s (mS.cm-1) |
| 17 | 10.95 |
| 18 | 11.19 |
| 19 | 11.43 |
| 20 | 11.67 |
| 21 | 11.97 |
| 22 | 12.15 |
| 23 | 12.39 |
| 24 | 12.64 |
| 25 | 12.88 |
Une fois l' appareil étalonné on peut commencer les mesures de L en fonction du volume d' agent titrant versé.
On peut se contenter aussi de suivre l' évolution de s en fonction du volume d' agent titrant versé.
Comme on a fait "comprendre" à l' appareil qu' il était étalonné on peut alors lire directement s pour calculer L.
Il faudra alors faire très attention aux unités
choisies pour la propriété qu' on suit: les siemens, ce ne
sont pas des siemens par mètre!
La conductivité s est
fonction des espèces en solution, ainsi que de leur concentration.
Chaque ion conduit le courant électrique avec
une certaine "agilité" qui lui est propre.
La contribution d' un ion de charge z, de concentration
Ci, à la conductivité globale d'une solution
ionique, est égale par définition à:
| Ion | l° (en S.m2.mol-1) |
| H3O+ | 3.50.10-2 |
| Na+ | 5.01.10-3 |
| K+ | 7.35.10-3 |
| NH4+ | 7.34.10-3 |
| HO- | 1.99.10-2 |
| F- | 5.54.10-3 |
| Cl- | 7.63.10-3 |
| Br- | 7.81.10-3 |
| I- | 7.70.10-3 |
| NO3- | 7.14.10-3 |
| HCO2- | 5.46.10-3 |
| CH3CO2- | 4.09.10-3 |
| SO42- | 1,6.10-2 |
| PO43- | 2,784.10-2 |
On pourra dès lors, aisément, suivre par conductimétrie l' évolution d' un dosage, en montrant qu' au cours d' un dosage des ions disparaissent, d' autres apparaissent, d' autres enfin restent spectateurs. L' effet global pourra permettre de déceler un point d' équivalence.
Exercice d'application:
Comparer le dosage d' une solution d' acide chlorhydrique
de concentration égale à 0.1 mol.L-1, de volume
égal à 100 mL, par la soude, de concentration égale
à 0.5 mol.L-1, par DEUX méthodes, la première
potentiométrique (pH métrie), la seconde étant conductimétrique.
En dosage par pH-métrie le volume équivalent se situe bien sûr à V = 20 mL de soude versée. L' équivalence est repérée par un saut de potentiel conséquent à V = 20 mL.
En conductimétrie on va exprimer la conductivité s de la solution en fonction de V, avant et après l' équivalence.
ATTENTION!!!
Il faudra exprimer toutes les concentrations en mol.m-3!!!!
afin d' assurer l' homogénéité des formules.
Avant et/ou après l' équivalence on aura:
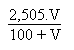 S.m-1
S.m-1
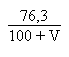 S.m-1
S.m-1
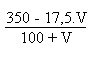 S.m-1
S.m-1Après l' équivalence, vu que les ions hydronium seront devenus négligeables devant les ions hydroxyde, on aura comme seul changement, vu que les conductivités des ions sodium et chlorure ont les mêmes expressions:
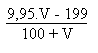 S.m-1
S.m-1On dressera un tableau des conductivités avant
et après équivalence, puis on insèrera un graphique
donnant l' évolution de s
totale en fonction de V.
| V (en mL) | s (en S.m-1) |
| 0 | 4.263 |
| 2 | 3.885 |
| 4 | 3.522 |
| 6 | 3.173 |
| 8 | 2.836 |
| 10 | 2.512 |
| 12 | 2.199 |
| 14 | 1.897 |
| 16 | 1.606 |
| 18 | 1.325 |
| 20 | 1.053 |
| 22 | 1.240 |
| 24 | 1.422 |
| 26 | 1.597 |
| 28 | 1.767 |
| 30 | 1.932 |
Le fait de remplacer les ions hydronium, très conducteurs, par des ions hydroxyde, moins conducteurs, conduit à une cassure au niveau de l' équivalence. On peut donc, par cette méthode, détecter un point d' équivalence acidobasique sans difficulté.
On pourra chercher à titre d' application, l' étude du dosage conductimétrique de l' hydroxyde de potassium, de concentration égale à 0.1 mol.L-1, de volume égal à 100 mL, par l' acide iodhydrique, de concentration égale à 0.5 mol.L-1.
On pourra également étudier le dosage par conductimétrie d' une solution d' acide éthanoïque, de concentration égale à 0.1 mol.L-1, de volume égal à 100 mL, par une solution aqueuse d' hydroxyde de sodium de concentration égale à 0.5 mol.L-1.
La méthode est donc complémentaire par rapport à la potentiométrie.
Retour au plan du cours sur les pH des solutions aqueuses.
Suite du cours sur les pH des solutions aqueuses. Cliquer ici.